Дипломная работа: Аналітичне дослідження кривошипно-шатунного механізма автомобільних двигунівДипломная работа: Аналітичне дослідження кривошипно-шатунного механізма автомобільних двигунівАналітичне дослідження кривошипно-шатунного механізма автомобільних двигунів Дипломна роботаВступДвигуни внутрішнього згорання належать до найбільш поширеного типу теплових двигунів. На їх долю припадає понад 80% всієї виробленої в світі енергії. Завдяки компактності, високій економічності, надійності і довговічності вони використовуються у всіх галузях народного господарства і є практично єдиним джерелом енергії на транспортних, будівельних і дорожних машинах. Головним напрямком розвитку сучасного автотракторного двигунобудування є підвищення питомих енергетичних і економічних показників, збільшення моторесурсу двигунів при одночасному зниженні питомої металоємкості, забезпечення роботи на недорогих видах палива, покращення економічних характеристик – зниження токсичності і димності відпрацьованих газів, зменшення питомих затрат на виготовлення, обслуговування і ремонт. Одним з шляхів вирішення цих завдань є удосконалення конструкції механізмів двигуна. Аналіз конструкції кривошипно-шатунних механізмів показує, що на багатьох двигунах використовують механізми, в яких вісь циліндра не перетинає вісь колінчастого вала, або у яких вісь поршневого пальця зміщена відносно осі циліндра. Такі механізми називають дезаксіальними. За даною схемою побудовані механізми двигунів ВАЗ усіх моделей, МеМЗ-968, ЗМЗ-51, ЗІЛ-130, М-20, СМД-60 та інших. Перевага дезаксіального механізма полягає у більш рівномірному зношуванню циліндрів за рахунок часткового перерозподілу сил, що діють на правий і лівий боки циліндра, а також меншу швидкість поршня в районі верхньої мертвої точки, що покращує процес горіння. Крім цього вирішується і ряд проблем компоновки двигуна. Проте в літературі не наведено результатів кінематичних і динамічних досліджень дезаксіального механізма, які б ілюстрували його переваги. В даній дипломній роботі поставлено завдання аналітичного дослідження аксіального і дезаксіального кривошипно-шатунного механізмів з метою виявлення якісного і кількісного впливу дезаксіалу на їх кінематичні і динамічні характеристики. Реалізація даного завдання вимагала проведення кінематичного і динамічного дослідження обох типів механізмів, побудови індикаторної діаграми робочого циклу двигуна, відповідних обчислень. При проведенні досліджень та обчислень було прийнято ряд припущень, спрощень і наближень: кутова швидкість w колінчастого вала постійна; маси тіл зосереджені в центрах ваги цих тіл; нехтування силою тертя; ідеалізація робочих процесів в циліндрі двигуна. Тому отримані результати в більшій мірі якісно ніж кількісно характеризують досліджувані процеси. 1. Термодинамічний і дійсний цикли поршневих двигунів внутрішнього згорання (ДВЗ) 1.1 Термодинамічний і теоретичний цикли поршневого ДВЗ Процеси перетворення теплоти в роботу можуть здійснюватися в різних теплових двигунах, одним з яких є поршневий ДВЗ. Термодинамічний (ідеальний) цикл – зворотній круговий процес, в якому теплота перетворюється в роботу з мінімальними втратами. Аналіз термодинамічних циклів поршневих ДВЗ проводиться з припущенням, що: 1) на протязі всього циклу ні хімічний склад, ні кількість робочого тіла (газу) не змінюється; 2) процеси стиску і розширення здійснюються адіабатично; 3) теплоємність робочого тіла не залежить від температури. Процеси горіння і газообміну, що протікають під час роботи реального поршневого двигуна, при розгляді термодинамічних циклів заміняються процесами підведення і відводу теплоти. Умови аналізу термодинамічних циклів такі, що отримані розрахункові значення їх показників являють собою деяку найвищу межу, до якої можуть лише наближатися показники дійсних циклів в залежності від ступеня їх досконалості. Ступінь досконалості теплових двигунів може бути оцінена шляхом співставлення їх дійсного робочого процесу з відповідним термодинамічним циклом. Загальноприйнятими теоретичними циклами поршневих ДВЗ є цикли Отто-Бо де Роша, Дизеля, Сабате-Трінклера. Ці цикли характеризуються наступними особливостями: 1) стиск починається у н.м.т.; 2) стиск і розширення здійснюються адіабатично з узагальненим постійним показником; 3) підведення і відведення теплоти проходить при V=const і P=const. Еталонний термодинамічний цикл повинен мати найбільший к.к.д. Параметри стану робочого тіла у визначаючій точці цього циклу (в точці кінця стиску) повинні бути близькі до параметрів стану робочого тіла в тій же ж точці дійсного робочого процесу ДВЗ. В дійсних процесах поршневих двигунів внутрішнього згорання стиск починається не у н.м.т., а пізніше, через запізнення закриття впускного клапана. Як правило, стиск здійснюється політропічно. Через це параметри стану робочого тіла у визначаючій точці в термодинамічних циклах нічого спільного не мають (при умові рівності ступенів стиску) з параметрами стану робочого тіла в тій же ж точці дійсних робочих процесів. Таким чином термодинамічні цикли Отто-Бо де Роша, Дизеля, Сабате-Трінклера не є еталонними і не можуть бути використані для оцінки ступеня досконалості робочого процесу ДВЗ. У 1948 році Н.І.Білоконь запропонував узагальнений теоретичний цикл (рис. 1), який позбавлений вказаних недоліків. В цьому циклі стиск починається не у н.м.т., а пізніше, як у дійсних процесах поршневих ДВЗ. Стиск в цьому циклі здійснюється політропічно з відведенням теплоти. Параметри стану робочого тіла у визначаючій точці циклу Н.І.Білоконя близькі до параметрів стану робочого тіла в цій же ж точці дійсного робочого процесу ДВЗ. Крім цього цикл Н.І.Білоконя в умовах найвигіднішого політропічного стиску має найбільший к.к.д. з всіх відомих термодинамічних циклів.
Рис.1 Узагальнений теоретичний цикл ДВЗ На основі цього узагальнений теоретичний цикл може бути використаний для оцінки ступеня досконалості дійсних робочих процесів ДВЗ і покладений в основу теплових розрахунків. Елементи узагальненого теоретичного циклу: а-с – найвигідніший політропічний стиск з відведенням теплоти, при якому к.к.д. циклу має найбільше значення; c-f-z – послідовний підвід теплоти при V=const і p=const; z-r – адіабатичне розширення; r-s-a - послідовний відвід теплоти при V=const і p=const 1.2 Дійсний цикл поршневих двигунів внутрішнього згорання Дійсним циклом поршневого двигуна внутрішнього згорання називають комплекс процесів, що періодично повторюються і здійснюються з метою перетворення термохімічної енергії палива в механічну роботу. Зміну тиску газів в циліндрі працюючого двигуна визначають з допомогою спеціального приладу – індикатора тиску, а отриману при цьому діаграму в координатах тиск – об’єм (p – V) або тиск – кут повороту колінчастого вала (р – j) називають індикаторною діаграмою. Індикаторна діаграма дійсного циклу чотиритактного бензинового двигуна наведена на рис.2. Цей цикл здійснюється за два оберти колінчастого вала або чотири такти (ходи поршня), під час яких в циліндрі відбуваються наступні процеси. Процес впуску паливної суміші починається в точці а¢, що відповідає початку відкриття впускного клапана, коли поршень ще не дійшов до в.м.т. Закінчується впуск в точці а¢¢, коли впускний клапан повністю закрився, а поршень пройшов н. м. т. Середній тиск газів в циліндрі на протязі впуску діє по напрямку руху поршня до н.м.т.; по значенню він менший за атмосферний р0, який перешкоджає руху поршня. Процес стиску заряду проходить після закінчення впуску (точка а¢¢) і супроводжується підвищенням температури і тиску заряду. При наближенні поршня до в.м.т. паливна суміш запалюється електричною іскрою (точка d). Процес горіння починається в точці d. В цей момент поршень на більшості режимів роботи двигуна ще не доходить до в.м.т. Момент закінчення цього процесу може знаходитись достатньо далеко після в.м.т. Прийнято вважати, що цей процес закінчується в точці z1. На протязі процесу горіння температура і тиск в циліндрі досягають найбільших значень. Процес розширення триває від точки z до точки b¢. При розширенні палива теплова енергія, що виділилась в результаті згорання палива, перетворюється в механічну. Процес випуску починається в точці b¢, що відповідає початку відкриття випускного клапана. Закінчується процес в точці b¢¢, після того, як поршень пройде в.м.т. і випускний клапан закриється. Процеси, під час яких проходить заміна робочого тіла – впуск і випуск називаються процесами газообміну. Поділ дійсного циклу на процеси дещо умовний, так як між закінченням попереднього і початком наступного процесів немає чіткої межі.
Рис. 2 Індикаторна діаграма дійсного циклу 1.2.1 Процеси газообмінуВід кількості і складу свіжого заряду в значній мірі залежить отримана в циклі робота, а відповідно, потужність двигуна. Кількість пальної суміші, що поступає в циліндри на протязі процесу впуску залежить від того, наскільки добре циліндри очищаються від відпрацьованих газів під час випуску в попередньому циклі. Таким чином впуск і випуск тісно взаємозв’язані. Випуск відпрацьованих газів починається в кінці розширення з випередженням 40 – 700 до приходу поршня в н.м.т. В цей момент тиск в циліндрі р » 0,4...0,6 МПа. Перший період процесу випуску називається періодом вільного випуску і закінчується біля н.м.т., коли випускний клапан є відкритим менше ніж на половину від свого максимального підйому. Під час другого періоду, тобто при русі поршня від н.м.т. до в.м.т., випуск відбувається під дією поршня. У випускній і впускній системах двигуна виникають коливальні процеси. Природа коливальних процесів в системах випуску і впуску має багато спільного. Досвід показує, що для кращого газообміну впускний клапан потрібно почати відкривати приблизно за 10 – 300 до приходу поршня в в.м.т., а випускний клапан закривати 100 – 500 після в.м.т. Період, коли одночасно відкриті обидва клапани, називають перекриттям клапанів. Під час перекриття клапанів в залежності від співвідношення значень тиску в циліндрі p, у впускному pВ і випускному pP трубках гази можуть рухатися в різних напрямках. В оптимальному випадку при pB<pP<p через впускний клапан в циліндр поступає свіжий заряд, а через випускний виходять відпрацьовані гази. Через деякий час після відкриття впускного клапана тиск в циліндрі і перед клапаном вирівнюються і з цього моменту починається впуск. Тиск в циліндрі в кінці газообміну pа = pВ – Dpа, де pВ – тиск у впускному трубопроводі, Dpа – опір впускної системи. Опір впускної системи визначається за залежністю Dpа = k1×w2 = k2×n2, де k1 i k2 – коефіцієнти пропорціональності, w – швидкість пальної суміші у впускній системі (w = 40 – 80 м/с), n – частота обертання колінчастого вала. Наближено опір впускної системи може бути визначений за емпіричною формулою Dpа = (0,05 – 0,1) pВ. Для дизелів приймаються нижчі значення коефіцієнта у даній залежності, для бензинових двигунів – вищі. Орієнтовні значення основних параметрів газообміну, визначених експериментально, наведені в таблиці 1. Таблиця 1
* pк – тиск наддуву 1.2.2 Процес стискуПри
термодинамічному розрахунку процесу стиску вважають, що він протікає на протязі
всього ходу поршня від н.м.т. до в.м.т. В теорії поршневих двигунів
внутрішнього згорання прийнято вважати, що стиск проходить політропічно з
постійним середнім показником n1 по рівнянню pc = pa
де e – ступінь стиску. Температура заряду в кінці стиску Tc = Ta
Орієнтовні значення параметрів кінця стиску і показника n1 подані в таблиці 2. Таблиця 2
* тиск наддуву pк £ 0,2 МПа 1.2.3 Процес горінняГоріння є складним фізико-хімічним процесом. На більшу частину показників двигуна впливають, однак, не фізико-хімічні особливості процесу горіння, а закономірності тепловиділення і викликаних ним зміни тиску і температури в циліндрі. Ними визначаються енергетичні і економічні показники циклу, статичні і динамічні навантаження на деталі, що оцінюються максимальним тиском циклу і швидкістю наростання тиску при горінні, теплова напруженість деталей. Задовільні показники роботи двигуна забезпечуються при тепловиділенні, що починається за 5 – 150 до в.м.т. і завершується через 45 – 500. Максимальний тиск робочого процесу бензинового двигуна визначається по формулі pz = lpc, де l – ступінь підвищення тиску в процесі горіння. Дійсне значення максимального тиску для карбюраторних двигунів рівне pzд » 0,85 pz. Параметри стану робочого тіла в кінці видимого горіння наведенні в таблиці 3. Таблиця 3
* верхні значення для двигунів з наддувом. 1.2.4 Процес розширенняВ процесі розширення здійснюється основна частина позитивної роботи циклу. Як і для процесу стиску, дійсний процес з змінним показником політропи може бути замінений умовним з середнім показником, який вибирають так, щоб тиски на початку і в кінці процесу були такими ж, як і в дійсному процесі. Параметри стану робочого тіла в кінці розширення наведені в таблиці 4. Таблиця 4
2. Кінематика кривошипно-шатунного механізма При роботі поршневого двигуна в його кривошипно-шатунному механізмі виникають сили, які визначають умови роботи окремих деталей, а також самого двигуна в цілому. Величина і характер зміни цих зусиль можуть бути визначені за допомогою рівнянь кінематики і динаміки кривошипно-шатунного механізма. Ці рівняння дозволяють також визначити точне положення для будь-якого кута повороту колінчастого вала, що дуже важливо для розрахунку процесів сучасних автомобільних і тракторних двигунів. При розгляді кінематики КШМ вважають, що кутова швидкість обертання колінчастого вала w постійна і, відповідно, кут його повороту пропорційний часу t. В деяких автомобільних і тракторних двигунах застосовують кривошипно-шатунний механізм, у якого вісь циліндра не перетинає вісь колінчастого вала, а зміщена відносно неї на деяку відстань. Такий механізм називають дезаксіальним. Дезаксіал також може бути отриманий зміщенням осі поршневого пальця. До переваг дезаксіального КШМ слід віднести: зменшення різниці в тиску поршня на праву і ліву сторони циліндра, що забезпечує більш рівномірне зношування двигуна; менша швидкість поршня біля В.М.Т., завдяки чому покращується процес згорання робочої суміші; при нижньому розміщені газорозподільного вала є можливість зменшити відстань між осями колінчастого і газорозподільного валів, а разом з тим діаметри розподільних шестерень і габарити картера привода. 2.1 Кінематика центрального кривошипно-шатунного механізма Схема центрального КШМ подана на рис.3. Залежність між кутом повороту колінчастого вала і відповідним йому часом є такою
де j – кут повороту колінчастого вала, град; t – час, що відповідає цьому куту, сек; n – число обертів колінчастого вала, об/хв. За вихідне приймаємо таке положення КШМ, при якому поршень знаходиться у верхній мертвій точці (в.м.т.). Вводимо такі позначення: r – радіус кривошипа; l – довжина шатуна; S=2r – хід поршня; s – шлях поршня (переміщення від в.м.т.), що відповідає повороту колінчастого вала на кут j; b – кут відхилення осі шатуна від осі циліндра. 2.1.1 Шлях поршня Визначимо залежність шляху поршня від відповідного кута повороту колінчастого вала. З рис.2 шлях поршня S рівний S = OA – OA1 або S = (r + l) – (r×cosj + l×cosb) = r×(1 - cosj) + l×(1 - cosb) = = r×[(1 - cosj) +
Рис.3 Схема центрального КШМ Ввівши позначення
S=r×[(1-cosj) + З рис.2 слідує,
що BC = r×sinj = l×sinb. Звідси sinb = Так як cosb=1 - В цій формулі значення членів, які включають величину l в степені вище першої, швидко зменшуються. Це дозволяє з достатньою для практики точністю обмежитися першими двома членами розкладу, тобто cosb = 1 – 0,5×l2×sin2j. (3) Тоді вираз для шляху поршня S = r×(1 - cosj) + Так як Після ряду перетворень отримаємо: S= r{(1 + 2.1.2 Швидкість поршня Наближену формулу для визначення швидкості поршня отримаємо, диференціюючи вираз (4) по часу:
Так як V = r×w×(sinj + 0,5×l×sin2j). (5) 2.1.3 Прискорення поршня Формулу для визначення прискорення поршня отримаємо диферент ціюванням виразу (5) по часу j = Звідси j = r×w2×(cosj + l×cos2j). (6) 2.2 Кінематика дезаксіального кривошипно-шатунного механізма Схема
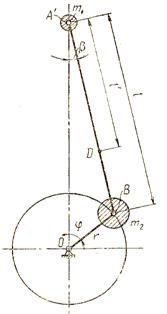
дезаксіального КШМ подана на рис.4. За вихідне приймаємо таке положення КШМ,
при якому кривошип займає вертикальне положення, а поршень знаходиться
практично у в.м.т. Вводимо нові позначення: e – дезаксіал; k = 2.2.1 Шлях поршняЗ рис.4 шлях поршня Sд рівний Sд = O1A – O1A¢,
O1A¢ = O1C + CA¢ = r×cosj + Тоді Sд = r×
Рис.4 Схема дезаксіального КШМ2.2.2 Швидкість поршняФормулу для визначення швидкості поршня отримаємо, диференцію-ючи вираз (7) по часу Vд = = r×w×( 2.2.3 Прискорення поршняФормулу для обчислення прискорення поршня отримаємо диференцію-ванням виразу (8) по часу jд =
3. Динаміка кривошипно-шатунного механізма 3.1 Сили, що діють в КШМСили, що діють в елементах КШМ двигуна, визначаються в результаті сумісної дії сил тиску газів Pr на поршень і сил інерції рухомих мас Pj. Закон зміни діючих сил в кожному циліндрі багатоциліндрового двигуна теоре-тично однаковий, тому аналіз сумарної дії сил можна провести на схемі сил, що діють в КШМ одноциліндрового двигуна (рис.5). Сумарна сила P, що діє на поршень, рівна P = Pr + Pj (10) Ця сила змінна по величині і напрямку і в залежності від кута повороту колінчастого вала може бути направлена до осі вала, або від неї. Сила Р, що діє по осі циліндра, розкладається на дві складові: силу N, перпендикулярну до осі циліндра і силу S, направлену по осі шатуна. Бокова сила N притискає поршень до лівої або правої частини стінки циліндра і викликає його зношу-вання. Сила S розтягує або стискає шатун і передається на шатунну шийку кривошипа N = P×tgb ; (11) S = P× Якщо перенести силу S по напрямку її дії в центр шатунної шийки S¢, то її можна розкласти на дві складові: тангенціальну силу Т, напрямлену перпендикулярно до радіуса кривошипа, і силу К – по його радіусу. Т = Р× К = Р× Сила Т створює обертовий момент Мкр =
Т×r
= P×r× Одночасно опори двигуна сприймають перекидаючий момент Мпр =
– N×h,
h = r× Перекидаючий момент рівний крутному з оберненим знаком Мпр = – Мкр
Рис.5 Схема сил, що діють в КШМ одноциліндрового двигуна3.2 Сили інерції КШМСили інерції мас, що здійснюють зворотно-поступальний рух, обчислюються за формулою Pj = – m×j (15) де m – маса чистин, які здійснюють зворотно-поступальний рух. Масу m вважають зосередженою в центрі пальця поршня. Маса частин, які здійснюють зворотно-поступальний рух, рівна m = mп + m1, де mп – маса комплектного поршня, включаючи маси власне поршня, поршневих кілець, поршневого пальця, m1 – частина маси шатуна, приведена до осі поршневого пальця. При динамічному дослідженні двигуна застосовують наближений спосіб визначення сил інерції шатуна, замінюючи на основі законів механіки рух фактичної маси шатуна mш рухом двох або кількох умовних мас. Для отримання системи, яка динамічно заміняє дійсну, необхідно дотриматись таких умов: сума всіх заміняючи мас повинна бути рівна масі шатуна; загальний центр ваги всіх заміняючи мас повинен співпадати з центром ваги шатуна і рухатись за законом руху цього центра ваги; сума моментів інерції всіх заміняючи мас відносно осі, що проходить через центр ваги шатуна, повинна бути рівна моменту інерції шатуна, відносно цієї ж осі; кутове прискорення заміняючої системи в обертовому русі по відношенню до центра ваги повинно бути рівне кутовому прискоренню шатуна в цьому ж русі. Замінимо масу шатуна двома масами m1 і m2 (рис.6). Умови приве-дення, необхідні для отримання системи, еквівалентної в динамічному відношенні системі шатуна, будуть мати вигляд mш = m1 + m2; m1×l¢ = m2×(l - l¢); (17) m1×l¢2 + m2×(l - l¢)2 = Jш. З умов (17) визначимо: m1 = mш× Для визначення мас mш, m1, m2 необхідно знати вагу шатуна, а також положення його центру ваги. Для готового шатуна ці величини визначаються способом зважування. Перше зважуванням визначають повну вагу шатуна Gш = G1 + G2, а потім зважуванням шатуна на двох опорах (рис.7), - різницю DG DG = G1 – G2 . Сумісний розв’язок цих рівнянь дозволяє визначити G1 і G2: G1 = 0,5×(Gш - DG), G2 = Gш – G1. (19) Відстань центру ваги шатуна від осі пальця поршня
Рис.6 Схема заміни маси шатуна двома масамиУ якості першого наближення при розрахунках можна прийняти: m1=(0,2…0,3)mш, m2=(0,7…0,8)mш, l¢=(0,7…0,8)l.
Рис.7 Визначення центру ваги шатуна методом зважування 3.3 Сили тиску газівСили тиску газів в циліндрі двигуна в залежності від ходу поршня визначають по індикаторній діаграмі, побудованій за даними теплового розрахунку, чи отриманої експериментально. Сила тиску газів на поршень діє по осі циліндра і рівна Рг = (рг – р0)×Fn (21) де рг – тиск газів в циліндрі двигуна, визначений для відповідного положення поршня по індикаторній діаграмі, р0 – тиск в картері, що приймається рівним тиску навколишнього середовища, Fn – площа поршня. Для динамічного розрахунку двигуна, а також для розрахунку на міцність його деталей необхідно мати залежність pг = ¦(j), для чого індикаторну діаграму перебудовують з координат p – V (рис.8а) в координати р - j (рис.8б) Зв’язок між кутом пороту колінчастого вала j і переміщенням поршня S зручніше виразити графічно, з врахуванням поправки на кінцеву довжину шатуна DS = Проекція кінця променя на вісь абсцис, проведеного з точки О1 під кутом j до цієї осі, дає положення поршня, відповідне цьому куту. Тиск газів, що відповідає даному куту j і положенню поршня, відкладається на діаграмі (рис.8б)
Рис.8 Схема переведення індикаторної діаграми з координат p – V в координати p - j 4. Дослідження кривошипно-шатунного механізма двигуна ВАЗ-2106 4.1. Вихідні дані для дослідження У даній роботі проведено кінематичне і динамічне дослідження кривошипно-шатунного механізма двигуна ВАЗ-2106. Даний механізм дезаксіальний. Геометричні і масові параметри деталей КШМ даного двигуна наведені в таблиці 4. Для оцінки впливу величини дезаксіалу на сили, що діють в КШМ, розрахунки проводились для значень е=-4...+4 мм, в тому числі і для центрального механізма (е=0). Таблиця 4
4.2. Кінематичний розрахунок кривошипно-шатунного механізма Кінематичний розрахунок центрального кривошипно-шатунного механізма проводився за формулами (2), (5), (6). Кінематичний розрахунок дезаксіального механізма – за формулами (7) – (9). Розрахунок проводився на ПК за програмами, наведеними в додатку 1. Результати розрахунків представлені в таблицях 1 – 9 додатку 2. Як показують результати розрахунків, у двигунах з дезаксіальним КШМ (при позитивному дезаксіалі) спостерігається зменшення швидкості поршня при його перебуванні в районі в.м.т. на такті розширення (0...30о повороту колінчастого вала). При значенні е=0.002 мм швидкість поршня зменшується на 2-7%, при значенні е=0.004 мм – на 4-11% у порівнянні з аксіальним КШМ (таблиця 5). Таблиця 5
4.3. Динамічний розрахунок кривошипно-шатунного механізма Сила інерції мас, що здійснюють зворотно-поступальний рух, обчислю-валась за формулою (15) Pj = – m×j. Маса частин, які здійснюють зворотно-поступальний рух, рівна m = mп + m1, де mп – маса комплектного поршня, включаючи маси власне поршня, поршневих кілець, поршневого пальця, m1 – частина маси шатуна, приведена до осі поршневого пальця. Маси поршня і шатуна визначалися зважуванням. Частина маси шатуна, приведена до осі поршневого пальця, приймалась рівною (згідно рекомендацій) m1 = 0.25mш. Прискорення мас, які здійснюють зворотно-поступальний рух, розраховано в розділі 4.3. Сила тиску газів на поршень визначалась за формулою (21) Рг = (рг – р0)×Fn. Значення тиску газів в циліндрі визначалось за індикаторною діаграмою. Так як в літературі не наводиться індикаторна діаграма робочого циклу двигуна ВАЗ-2106, проводилась побудова наближеної діаграми для даного двигуна. За основу взято наведену в [6] індикаторну діаграму робочого циклу чотиритактного бензинового двигуна і трансформовано її в індикаторну діаграму досліджуваного двигуна з врахуванням значень тиску у базових точках. Такими є наступні точки: точка а – тиск в кінці такту впуску, точка с – тиск в кінці такту стиску, точка z – максимальний тиск в циліндрі в кінці процесу горіння, точка b – тиск на початку процесу випуску. З врахуванням даних, наведених в таблицях 1-4, а також параметрів двигуна, тиск в базових точках рівний: pа = pв – Dpа = pв – 0.1pв = 0.9pв = 0.9*0.108 = 0.093 МПа; pc = pa
pz = 0.85lpc = 0.85 * 3.9 * 1.64 = 5.4 МПа; pb=0.35 МПа. Побудована за такими даними діаграма наведена на рис.9. Значення сили тиску газів через 10о повороту колінчастого вала наведено в таблицях додатку 4 і позначено як P1. Сила інерції мас, що рухаються зворотно-поступально, позначена в цих таблицях як Р2. Сила N, яка притискає поршень до стінки циліндра, обчислювалась за формулою (11) N = P×tgb. Значення кута b для аксіального кривошипно-шатунного механізма виходячи з розрахункової схеми, наведеної на рис.2, розраховувалось як
Значення кута b для дезаксіального кривошипно-шатунного механізма виходячи з розрахункової схеми, наведеної на рис.3, розраховувалось як
Результати розрахунку сили N представлені в таблиці 5. За отриманими результатами побудовано графічні залежності сили N від кута повороту колінчастого вала двигуна при різних значеннях дезаксіалу (рис.10). Як видно з рисунка, максимальне значення бокової сили N при русі поршня з в.м.т. до н.м.т. при такті розширення зменшується на 10% при е=0.002 мм і на 19% при е=0.004 мм в порівнянні з аксіальним механізмом. При русі поршня з н.м.т. до в.м.т. при такті стиску ця сила зростає відповідно на 9% і 17%. Нерівномірність навантаження k стінок циліндра визначалась як частка від ділення максимальної бокової сили при такті розширення до максимального її значення при такті стиску. Для аксіального механізма нерівномірність навантаження становить k=3,85, для дезаксіального при значенні е=0.002 мм k=3,13, при значенні е=0.004 - k=2,63.
Таблиця 5
Висновки 1. Отримано розрахункові залежності для визначення переміщення, швидкості і прискорення поршня для дезаксіального кривошипно-щатунного механізма автомобільного двигуна. 2. Кінематичний аналіз КШМ показав, що в дезаксіальному механізмі швидкість поршня в районі в.м.т. на такті розширення на 2-11% нижча у порівнянні з центральним механізмом. 3. Динамічний аналіз КШМ показав, що: а) в дезаксіальному механізмі бокова сила N на такті розширення на 5-19% нижча у порівнянні з центральним механізмом; б) нерівномірність навантаження стінок циліндра зменшується з k=3,85 у центральному механізмі до k=2,63 у дезаксіальному при значенні е=0,004 мм. 4. Отримані результати у дещо спрощеному варіанті можна використати для формулювання завдання на учбово-дослідну роботу під час лабораторного практикуму з курсу “Автомобілі і трактори”. Література1. Автомобильные и транспортные двигатели. Ч.І. Теория двигателей и системы их топливоподачи. – М.: Высш. школа, 1976. – 368с. 2. Автомобильные и транспортные двигатели. Ч.ІІ. Конструкция и расчет двигателей. Под ред. И. М. Ленина – М.: Высш. школа, 1976. – 280с. 3. Богданов С. К., Буренков М. М., Иванов И. Е. Автомобильные двигатели. – М.: Машиностроение, 1987. – 368с. 4. Вешкельский С.А., Лукьянченко Б.С. Техническая эксплуатация ДВС. –Л.: Машиностроение, 1986. 5. Двигатели внутреннего сгорания. Устройство и работа поршневых и ком-бинированных двигателей. Под. Ред. А.С.Орлина, М.Г.Круглова. –М.: Машиностроение, 1980. –288 с. 6. Двигатели внутреннего сгорания /Хатян А. С., Морозов К. А., Луканин В. К. и др. – М.: Высш. школа, 1985. – 311 с. 7. Поршаков Б.П., Романов Б.А. Основы термодинамики и теплотехники. –М.:, Недра, 1982. 8. Райков И.Я., Рытвинский Г.Н. Конструкция автомобильных и тракторних двигателей. – М.: Высш. Школа, 1986. –352 с. 9. Романов Б. А. Двигатели внутреннего сгорания. – М.: Недра, 1989 – 172с. ДОДАТКИ Додаток 1Програма розрахунку кінематичних характеристик аксіального КШМ pi=3.14159265359 kp=pi/180: коефіцієнт переводу градусів у радіани r=0.04 l=0.25 n=3000 w=pi*n/30 open "ZAD_1.TXT" for output as #1 print #1, " Fi"," S"," V"," j" for fiGrad=0 to 360 step 10 fi=kp*fiGrad S=r*((1+0.25*l)-(cos(fi)+0.25*l*cos(2*fi))) V=r*w*(sin(fi)+0.5*l*sin(2*fi)) j=r*w^2*(cos(fi)+l*cos(2*fi)) print #1, fiGrad, print #1, using "-#.######";S,:print #1, , print #1, using "-##.###";V,:print #1, , print #1, using "-####.###";j next end Програма розрахунку кінематичних характеристик дезаксіального КШМ pi=3.14159265359 kp=pi/180: коефіцієнт переводу градусів у радіани r=0.04 l=0.25 n=3000 w=pi*n/30 open "ZAD_2.TXT" for output as #1 e=0.001 gosub 100 e=0.002 gosub 100 e=0.003 gosub 100 e=0.004 gosub 100 end 100 k=25*e print #1, "e="; using "#.###";e print #1, print #1, " Fi"," S"," V"," j" for fiGrad=0 to 360 step 10 fi=kp*fiGrad A=l^(-2)-(sin(fi)-k)^2 S=r*(((1+1/l)^2-k^2)^0.5-A^0.5-cos(fi)) V=r*w*((sin(fi)-k)*cos(fi)/A^0.5+sin(fi)) j=r*w^2*((((cos(fi))^2-sin(fi)*(sin(fi)-k))*A+((cos(fi))^2)*(sin(fi)-k)^2)*A^(-1.5)+cos(fi)) print #1, fiGrad, print #1, using "-#.######";S,:print #1, , print #1, using "-##.###";V,:print #1, , print #1, using "-####.###";j next print #1, return_ Додаток 2 Аксіальний КШМ (е = 0)
Дезаксіальний КШМ (е = 0,001 м)
Дезаксіальний КШМ (е = 0,002 м)
Дезаксіальний КШМ (е = 0,003 м)
Дезаксіальний КШМ (е = 0,004 м)
Дезаксіальний КШМ (е = – 0,001 м)
Дезаксіальний КШМ (е = – 0,002 м)
Дезаксіальний КШМ (е = – 0,003 м)
Дезаксіальний КШМ (е = – 0,004 м)
Додаток 3 Програма розрахунку динамічних характеристик аксіального КШМ pi=3.14159265359 kp=pi/180: коефіцієнт переводу градусів в радіани r=0.04 l=0.25 n=3000 data 8328,26455,17881,13472,10288,8083,6614,5389,4654,3919,3307,2694, 2205,1837,1592,1225,1102,857,735,-490,-441,-367,-294,-245,0,122,245,490, 857,1225,1715,2205,2939,3429,4287,5389,8328 w=pi*n/30 open "ZAD_1.TXT" for output as #1 print #1, " Fi"," j"," p1"," p2"," N" for fiGrad=0 to 360 step 10 fi=kp*fiGrad S=r*((1+0.25*l)-(cos(fi)+0.25*l*cos(2*fi))) V=r*w*(sin(fi)+0.5*l*sin(2*fi)) j=r*w^2*(cos(fi)+l*cos(2*fi)) p2=-0.663*j read p1 z=(r*sin(fi))/l t=z/sqr(1-z^2) p=p1+p2 N=p*t print #1, fiGrad, print #1, using "-#####.##";j,:print #1, , print #1, using "-######.#";p1,:print #1, , print #1, using "-#####.##";p2,:print #1, , print #1, using "-#####.##";N next end_ Програма розрахунку динамічних характеристик дезаксіального КШМ pi=3.14159265359 kp=pi/180: коефіцієнт переводу градусів в радіани r=0.04 : l=0.25 n=3000 data 8328,26445,17881,13472,10288,8083,6614,5389,4654,3919,3307,2694,2205, 1837,1592,1225,1102,857,735,-490,-441,-367,-294,-245,0,122,245,490,857,1225, 1715,2205,2939,3429,4287,5389,8328 w=pi*n/30 open "ZAD_2.TXT" for output as #1 e=0.001 gosub 100 e=0.002 gosub 100 e=0.003 gosub 100 e=0.004 gosub 100 end 100 k=25*e print #1, "e="; using "#.###";e print #1, print #1, " j"," p1"," p2"," N" restore for fiGrad=0 to 360 step 10 fi=kp*fiGrad read p1 A=l^(-2)-(sin(fi)-k)^2 S=r*(((1+1/l)^2-k^2)^0.5-A^0.5-cos(fi)) V=r*w*((sin(fi)-k)*cos(fi)/A^0.5+sin(fi)) j=r*w^2*((((cos(fi))^2-sin(fi)*(sin(fi)-k))*A+((cos(fi))^2)*(sin(fi)-k)^2)*A^(-1.5)+cos(fi)) p2=-0.663*j z=(r*sin(fi)-e)/l t=z/sqr(1-z^2) p=p1+p2 N=p*t print #1, fiGrad, print #1, using "-####.##";j,:print #1, , print #1, using "-#####.##";p1,:print #1, , print #1, using "-####.##";p2,:print #1, , print #1, using "-####.##";N next print #1, return_ Додаток 4 Аксіальний КШМ (е=0)
Дезаксіальний КШМ (e=0.001 м)
Дезаксіальний КШМ (e=0.002 м)
Дезаксіальний КШМ (e=0.003 м)
Дезаксіальний КШМ (e=0.004 м)
Дезаксіальний КШМ (e=-0.001 м)
Дезаксіальний КШМ (e=-0.002 м)
Дезаксіальний КШМ (e=-0.003 м)
Дезаксіальний КШМ (e=-0.004 м)
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||


 , (1)
, (1)
 , то S » r×(1 - cosj) +
, то S » r×(1 - cosj) + 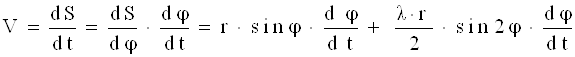
 = r×w×cosj×
= r×w×cosj×
 .
. - r×
- r× - r×cosj. (7)
- r×cosj. (7)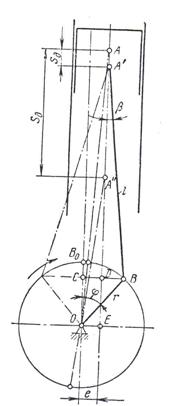
 + r×sinj)×w =
+ r×sinj)×w =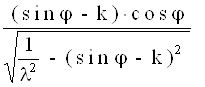 + sinj). (8)
+ sinj). (8) = r×w2 *
= r×w2 *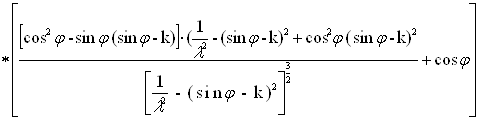 (9)
(9) (12)
(12)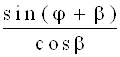 (13)
(13) (14)
(14)
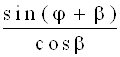 .
.
 (20)
(20)