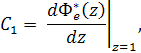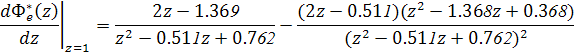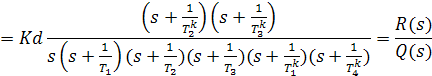Контрольная работа: Анализ систем автоматического управленияКонтрольная работа: Анализ систем автоматического управленияМинистерство образования Республики Беларусь Белорусский Государственный Университет Информатики и Радиоэлектроники Факультет Информационных Технологий и Управления Кафедра систем управления Курсовая работа по курсу: Теория автоматического управления Тема: Анализ систем автоматического управления Выполнил:Проверил: Студент гр. 722401Кузнецов А. П. Царик А.С. Минск 2010 Содержание 1. Исследование линейной непрерывной системы автоматического управления 2. Исследование линейной импульсной системы автоматического управления 3. Исследование нелинейной непрерывной системы автоматического управления Литература 1.Исследование линейной непрерывной системы автоматического управления Задание: 1)
Найти
передаточную функцию разомкнутой системы W(s) и передаточную функцию замкнутой
системы Ф(s),
2)
Построить
область устойчивости системы в плоскости общего коэффициента передачи К = К1К2К3
и постоянной времени Т2 при заданных значения Т1 и Т3.
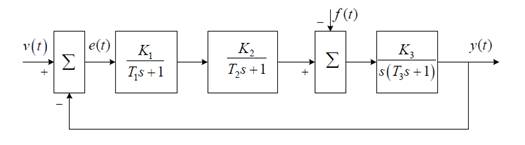
Найти граничное значение 3) Построить графики логарифмических амплитудной и фазовой частотных характеристик L(w) и φ(w) при значении коэффициента передачи K=0,7K’. 4) Оценить запасы устойчивости по модулю ∆L и фазе ∆ φ, величину ошибки по скорости еск при v(t) = v1t и f= 0, время переходного процесса tp и перерегулирование σ в исходной системе при K=0,7K’. 5) Если исходная система не удовлетворяет заданным в таблице 1 показателям качества tp, σ, еск (хотя бы одному из них) или имеет малые запасы устойчивости, то провести коррекцию системы (последовательного или параллельного типа) и найти передаточную функцию корректирующего устройства. 6) Вычислить в скорректированной системе переходный процесс на выходе y(t) при подаче на вход единичной ступенчатой функции v(t)=1(t)( f= 0). Найти tp, σ по переходному процессу и сравнить их с требуемым по заданию. Исходные данные: Структура исследуемой замкнутой линейной непрерывной САУ представлена на рис. 1.1, где v(t)- управляющее воздействие, (f)- возмущающее воздействие, е(t)- сигнал ошибки, y(t)- выходной сигнал. Значения параметров Т1 Т2, Т3 заданы в табл. 1. Размерность Т1 Т2, Т3 в секундах, общий коэффициент передачи К = К1К2К3 имеет размерность 1/с, в табл. 1 заданы также желаемые показатели качества системы: максимальная ошибка по скорости еск при скачке по скорости v(t) = v1t и f= 0, время переходного процесса tп.п в секундах, и перерегулирование у в процентах. Таблица 1. Структура исследуемой замкнутой линейной непрерывной САУ
Рисунок 1.1 Выполнение: 1. Требуемые передаточные функции находят с использованием правил структурных преобразований. Коротко сформулируем основные правила: — Передаточные функции последовательно соединенных звеньев перемножаются. — Передаточные функции параллельно соединенных звеньев складываются. Передаточная функция системы с обратной связью - это передаточная функция замкнутой системы, которая определяется по формуле:
Передаточная функция разомкнутой системы W(s) = Y(s)/U(s) при f= 0, e = u (т.е. разомкнута главная обратная связь) определится выражением:
где обозначим К = К1К2К3,
Главная передаточная функция или передаточная функция замкнутой системы при f = 0:
Передаточная функция по ошибке при f= 0, которая позволяет выразить ошибку e(t) в системе при известном входном воздействии:
Передаточная функция по возмущению при и = 0 позволяет выразить влияние возмущения на выходной сигнал:
2. . Передаточная функция разомкнутой исходной системы имеет вид W(s) = K/sL(s), где L(s) = (T1s+1)(T2s +1)(T3s+1). Характеристическое уравнение замкнутой системы будет D(s) = K+L(s)s = b0s4 +b}s3 +b2s2 +b3s + b4 =0, где при заданных из таблицы исходных данных числовых значениях Т1 и Т3 коэффициенты bj будут зависеть от параметров К и Т2. Применение критерия Гурвица к характеристическому уравнению четвертого порядка дает следующие условия устойчивости: b3(b1b2-b0b3)-b4b12 > 0, b, > 0, i = 0,...,4. Приравнивая в написанных соотношениях правые части нулю, найдем зависимость К от Т2 и построим в плоскости К и Т2 границы устойчивости, ограничивающие некоторую область устойчивости. При заданном параметре Т2 находим граничное значение КГР коэффициента передачи К.
К = К1К2К3 b0=
b3=1 b4=K Выразим К через параметр Т2:
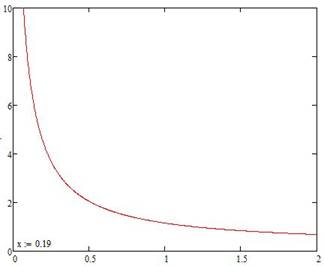
Зависимость К(Т2) приведена на рис. 1.2
Рис.1.2 Kгр=KT2=0.19=4,633 3. Полагая К = 0.7КГР, записываем аналитическое выражение для φ(w)= argW(jw), L(w) = 20lg|W(jw)| из W(s) при s = jw. К=0.7Кгр= 3,243 Передаточную функцию разомкнутой системы можно записать в виде:
где
тогда:
где
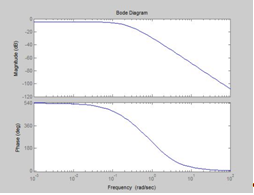
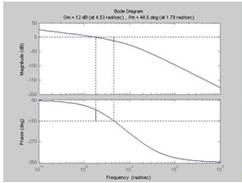
Строим графики логарифмических характеристик разомкнутой системы, с помощью MATLAB (оператор bode или margin) Рис. 1.3 а.
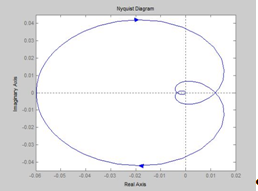
Рис. 1.3а Строим график АФЧХ с помощью MATLAB (оператор nyquist) рис. 1.3 б для разомкнутой системы.
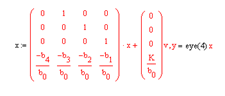
Рис 1.3 б Запасы устойчивости по модулю и фазе определяются по логарифмическим характеристикам (см. рис. 1.3 а): на частоте среза wс определяется запас по фазе —∆φ, а запас по амплитуде ∆L - на частоте при которой φ(w) = -180. Таким образом, ∆L≈0. 1дБ, ∆φ≈ 0°, что является недостаточным. 4. Величина ошибки по скорости определяется как eск=V1/K. Для ориентировочной оценки tпп и σ следует построить переходной процесс h(t) (оператор step в MATLAB) при v(t) = 1[t] и по нему определить tпп и σ. Для получения уравнений состояний в нормальной форме используем дифференциальное уравнение замкнутой системы D(s)y(t)=Kv(t). Если D(s)=b0s4+b1s3+b2s2+b3s+b4=0, ,то уравнение состояния имеет вид
Для описания динамических систем в пространстве состояний в Matlab применяются модели подкласса ss, которые основаны на линейных дифференциальных или разностных уравнениях. Модель непрерывной системы в подклассе ss имеет вид:
где: х - вектор состояния; v- вектор входа; у - вектор выхода. Для формирования моделей в подклассе ss предназначена функция ss sys=ss(A,B,C,D) В результате под именем sys получаем ss-объект с числовыми характеристиками в виде четверки матриц {А, В, С, D}, которые должны иметь согласованные размеры. Матрицу D в данном случае полагаем равной 0. Для построения переходного процесса h(t) воспользуемся оператором step в MATLAB. Реализация функций имеет вид: sys=ss([0 1 0 0;0 0 1 0;0 0 0 1;-b4/b0 -b3/b0 -b2/b0 -b1/b0],[0 0 0 K/b0]', eye(4), zeros(4,1)) a = x1 x2 x3 x4 x1 0 1 0 0 x2 0 0 1 0 x3 0 0 0 1 x4 -104.6 -32.26 -168.5 -36.16 b = u1 x1 0 x2 0 x3 0 x4 104.6 c = x1 x2 x3 x4 y1 1 0 0 0 y2 0 1 0 0 y3 0 0 1 0 y4 0 0 0 1 d = u1 y1 0 y2 0 y3 0 y4 0 Continuous-time model. >> step(sys) В результате получим графики представленные на рис. 1.4. Нас будетинтересовать Out(l). Величина ошибки по скорости определяется как: еск=V1/K = 1,4/3,243 = 0,432>ескзад = 0,04. Для ориентировочной оценки tnn и о следует построить переходной процесс h{t) (оператор step в MATLAB) при v(t)=1(t) и по нему определить tпп и σ. Эти величины из графика Out(l) определяются следующим образом:
Время переходного процесса определяется с учетом следующих соотношений: εуст=v(t)/(l+K), где v(t)=l[t], а К=3,243 - общий коэффициент передачи разомкнутой системы. Тогда еуст= 1/(1+3,243)=0,236 и следовательно tпп из графика Out(l) tпп ≈50с > tппзад = 2.5с.
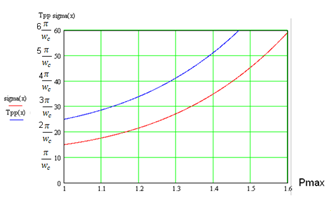
Рис 1.4 Таким образом, исходная система не удовлетворяет заданным показателям качества, ее следует скорректировать. 5. Если исходная система не удовлетворяет заданным показателям качества, ее следует скорректировать. В случае применения частотных методов синтеза коррекции строится желаемая ЛАЧХ Lж(w). В низкочастотной части желаемой ЛАЧХ при сохранении порядка астатизма (наличие интегратора 1/s в системе) требуемый коэффициент усиления выбирается из соотношения Kz=v1/eск=1,4 / 0.04 = 35. На частоте среза желательно иметь наклон ЛАЧХ -20 дБ/дек с протяженностью этого участка не менее одной декады. Далее среднечастотная часть ЛАЧХ сопрягается с низкочастотной отрезком прямой с наклоном -40(если необходимо -60) дБ/дек, а высокочастотная часть желаемой и исходной ЛАЧХ по возможности должны совпадать. Учет требований качества переходного процесса: tпп и σ, запасов устойчивости учитываются при формировании среднечастотной области Lж(w). Здесь можно воспользоваться графиком (рис. 1.5).
Рис 1.5 По графику рис. 1.5 для заданных значений у и tnn находим wп, и затем из соотношения wc = (0.6 - 0.9) wп, частоту среза wc. В наше случае: (как показано на рис.1.5) для у =10%, tр=3π/ωп ,откуда для tр значение ωп= 3π/1,5=6,8 1/с и ωc=5 1/с. Сопряжение среднечастотного участка с низкочастотным и высокочастотным (рис. 1.6) должно быть таким, чтобы была проще коррекция и чтобы изломы, по возможности, были не более чем на 20 дБ/дек (протяженность участка около декады). Тогда, выберем L2≈10дБ на частоте ω2=(0.1-0.5)ωс=2.5<ωс=5 и L3≈ -10 дБ на частоте ω3=25 ≥ ωс=5. Введем обозначения:
Величину ω1 найдем из условия равенства значений Lж(ω1)=Lисх(ω1). Это соотношение приводит к следующему выражению:
В последнем выражении обозначено: ω’=0.1w2 L’(ω’)=50 дБ L’(ω2)=10 дБ L(ω3p)=L(0.476)=21,18 дБ L(ω2)=L(1.2)=-35,743 дБ Последние две величины находятся из выражения для Lисх(w). Найденное по формуле значение ω1=0.098 ЛАЧХ корректирующего устройства с характеристикой Lk(w) соответствует функция:
где:
Общая передаточная функция разомкнутой системы с корректирующим звеном последовательного типа имеет вид:
Далее воспользуемся функцией zpk(z, р, К), где z и р - векторы из нулей и полюсов, a Kd - обобщенный коэффициент передачи, sys - любое имя присваиваемое модели. Тогда запись в системе Matlab примет вид: sys1=zpk([-1/t2k -1/t3k],[0 -1/t1 -1/t2 -1/t3 -1/t1k -1/t4k],kd) Zero/pole/gain: 58.2 (s+2.5) (s+0.4762) ------------------------------------------------- s (s+7.143) (s+4.167) (s+25) (s+0.4762) (s+0.097)
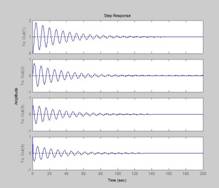
Рис. 1.6 6. Для нахождения переходных характеристик замкнутой системы с корректирующим звеном предварительно сформируем модель в пространстве состояний. Передаточная функция замкнутой системы имеет вид:
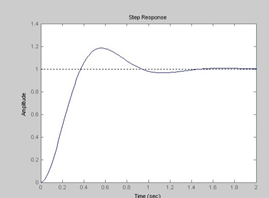
Для нахождения Ф(s) воспользуемся следующей последовательностью команд: >>sys1=zpk([-1/t2k -1/t3k],[0 -1/t1 -1/t2 -1/t3 -1/t1k -1/t4k],kd) Zam_ck=inv(l+sysl)*sysl - находится передаточная функция замкнутой системы. (Не оптимальная форма т.к. при такой последовательности команд не производится упрощение за счет сокращения одинаковых элементов числителя и знаменателя. В тоже время на результат дальнейшего расчета это не влияет). >>Zam_ck=inv(1+sys1)*sys1 Переходная характеристика (рис. 1.7 ) находится с помощью функций: 0,05 Из рассмотрения рис. 1.7 видно, что параметры по заданию выполняются.
Рис 1.7 Для устранения неоптимальности записи в Zam_ck=inv(l+sysl)*sysl можно в диалоговом режиме произвести новую запись zpk(.) - сокращая одинаковые элементы числителя и знаменателя в Zam_ck. 2.Исследование линейной импульсной системы автоматического управления Задание: 1) Найти передаточные функции импульсной САУ: W*(z) разомкнутой системы, Ф*(z) – замкнутой системы, Фе*(z) – системы по ошибке. Параметры Т, Т1, τ1, К0, γ входят в выражения передаточных функций в общем виде, т. е. в буквенном виде. Знак «*» будет относиться к передаточным функциям импульсной системы. 2) Найти интервал изменения коэффициента передачи К0, при котором система будет устойчива: K0”≤K0≤K’. Для дальнейших исследований выбрать значение K0=0.5K0’ 3) Построить графики логарифмических частотных характеристик разомкнутой импульсной системы L*(λ) и φ*(λ) при заданных значениях Т, Т1, τ1, γ и выбранном K0. По графикам определить запасы устойчивости системы по модулю ∆L* и фазе ∆φ*. 4) Определить ошибку системы по скорости еск при входном воздействии v(t)=t (скачок по скорости), а также первые два коэффициента ошибок с0 и с1. 5) Вычислить переходной процесс в системе при воздействии v(t)=1[t] (скачок по положению. Исходные данные: Таблица 2. Анализ одноконтурного замкнутого импульса
Анализируется одноконтурная замкнутая импульсная САУ, состоящая из непрерывной части (НЧ) и импульсного элемента (ИЭ), формирующего прямоугольные импульсы длительностью τ=γТ, где Т -период дискретизации, 0≤γ≤1. Исходные данные для расчетов приведены в таблице 2. Передаточная функция непрерывной части имеет вид:
Импульсный элемент представляется в виде идеального ключа и формирующего устройства с передаточной функцией:
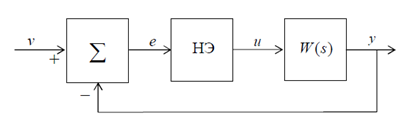
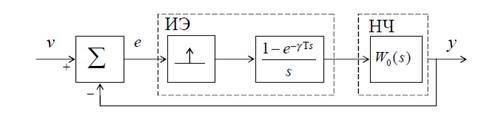
Структурная схема системы представлена на рис. 2.1. В табл. 2 Т, Т1, τ -постоянные времени имеют размерность секунды, К0 - коэффициент передачи НЧ имеет размерность сек-1 и выбирается далее.
Рис 2.1 Структурная схема линейной импульсной системы 1. Для нахождения передаточной функции разомкнутой импульсной САУ W*(z) находим передаточную функцию приведенной непрерывной части:
К W(s) применяется Z-преобразование и получается передаточная функция импульсной системы W*(z) = Z{W (s)}. Преобразуем W0(s) к виду:
Представим W0(s) в виде суммы двух слагаемых Применим к W0(s) Z-преобразование
Полученную передаточную функцию в конечном виде можно представить следующим образом:
где обозначено
Передаточные функции замкнутой системы находятся по выражениям:
2. Устойчивость системы определяется корнями характеристического уравнения замкнутой системы D*(z) = l + W*(z) = 0, которое для нашего случая будет иметь вид:
В соответствии с алгебраическим критерием замкнутая система будет устойчива при выполнении неравенств
В неравенстве при известных значениях γ, Т, τ1, Т1 входит величина К0. Таким образом, можно выделить отрезок значений К0"<К0 <К0, при которых система будет устойчива и далее принять К0 = 0.5К'0. Условия устойчивости будут:
После преобразований и возврата к старым переменным получим:
Получим 0<К0<7,112. Таким образом, принимаем К0=0.5 К0’=3,56. 1. Для построения частотных и логарифмических частотных характеристик в выражении W* (z) делаем замену переменной
В результате этого получим частотную характеристику W*(jλ) и далее логарифмическую амплитудно-частотную характеристику L*(λ) = 20Lg|W*(jλ)| и фазочастотную характеристику φ*(λ)= argW*(jλ), графики которых строятся в логарифмическом масштабе. Передаточная функция разомкнутой системы имеет вид
Тогда можно воспользоваться следующей последовательностью команд в MATLAB: >> sys=tf([0.231 0.085],[1 -(1/2.71+1) 1/2.71],1) Transfer function: 0.231 z + 0.085 --------------------- z^2 - 1.369 z + 0.369 >> sys_tr=d2c(sys,'tustin') Transfer function: -0.05332 s^2 - 0.1242 s + 0.4616 -------------------------------- s^2 + 0.9218 s + 2.047e-016 (опция 'tustin’ предназначена для преобразования Получаем выражение:
где параметры g и f видны из вышеприведенного выражения.
Рис 2.2 4. Рассматриваемая система для всех вариантов является астатической с астатизмом первого порядка и имеет следующую передаточную функцию:
В силу астатизма первого порядка в такой системе статическая ошибка всегда равна нулю, а скоростная еск вычисляется по формуле:
и следовательно, еск=1,999. Вычислим коэффициенты ошибок. Величина С0 =0, а коэффициент ошибки
Где Тогда получим производную:
Подставив в последнее выражение найденные ранее значения и z=1, окончательно получим С1=1,999. 5. При входном воздействии вида v(k) = l[k] переходный процесс в замкнутой системе можно вычислить с помощью моделирования импульсной системы в Matlab. Для этого необходимо задать передаточную функцию непрерывной части системы в tf- или zpk -форме, преобразовать ее в дискретную с помощью оператора c2d при заданном времени дискретизации T, а затем построить переходной процесс системы оператором step. Так же можно построить и логарифмические частотные характеристики импульсной системы -bode. Если задана передаточная функция замкнутой системы в виде:
и периодом дискретизации γT, то получим >> w0=tf([0.3 1 0],[0.3 1 1.411]) Transfer function: 0.1 s^2 + s ------------------- 0.1 s^2 + s + 3.738 0.2 >> w1=c2d(w0,0.24) Transfer function: z^2 - 0.8801 z - 0.1199 ------------------------ z^2 - 0.4001 z + 0.09072 Sampling time: 0.24 >> step(W1)
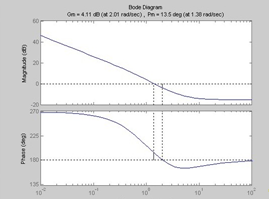
Рис 2.3 На рис.2.4 представлена диаграмма Боде исследуемой дискретной системы с отмеченными на ней запасами устойчивости по амплитуде и фазе.
Рис. 2.4 3.Исследование нелинейной непрерывной системы автоматического управления Задание: Используя метод гармонической линеаризации нелинейного элемента, определить на основе частотного способа возможность возникновения автоколебаний в замкнутой системе, их устойчивость, амплитуду и частоту. Исходные данные: Структура нелинейной САУ представлена на рис. 3.1, где НЭ— нелинейный элемент, W(s) - передаточная функция непрерывной линейной части системы.
Рис 3.1 1. Передаточная функция W0(s) берется из пункта 1, как передаточная функция скорректированной системы с соответствующими числовыми коэффициентами. Нелинейный элемент НЭ имеет нелинейную характеристику u=f(e) которая для всех заданий является характеристикой идеального реле:
где с=2. Приближенная передаточная функция нелинейного элемента для случая идеальное реле имеет вид:
где a – амплитуда искомого периодического режима, а>0. 2. На комплексной плоскости строим характеристику:
Это прямая, совпадающая с отрицательным отрезком действительной оси, вдоль которой идет оцифровка по амплитуде а0 = 0, a1, a2, …. В том же масштабе на комплексной плоскости строится АФЧХ разомкнутой системы W0(jw) при изменении частоты от 0 до + inf. Передаточная функция скорректированной системы:
На рис.3.2 (выделен интересующий фрагмент) пунктиром отмечена АФЧХ
рис.3.2 Точка пересечения кривых (-0,165; -0j). В точке пересечения АФЧХ W0(jw) и прямой
Приравнивая Im(W0(jw))=0 находим w*=1,065 (функция fsolve). При найденном значении
частоты получим Re(W0(jw*))=-1,3. Из условия Re(W0(jw*))= Для определения устойчивости периодического режима можно воспользоваться следующим правилом: если при увеличении
амплитуды а вдоль кривой Таким образом, периодический режим будет устойчивым. Литература 1. Теория автоматического управления. Конспект лекций: В 2ч. Ч.1: Линейные непрерывные системы : учеб.-метод. Пособие /В.П.Кузнецов,С.В.Лукьянец,М.А.Крупская.-Мн.:БГУИРб2007.-132с. 2. Кузнецов В.П. Линейные непрерывные системы: Тексты лекций по курсу: Теория автоматического управления.-Мн.:БГУИР,1995.-180с. 3. Электронный учебно-методический комплекс: Теория автоматического управления. Ч.1: Линейные непрерывные системы./ В.П. Кузнецов, С.В. Лукьянец, М.А. Крупская- Мн.:БГУИРб2006. 4. Электронный учебно-методический комплекс: Теория автоматического управления. Ч.2:Дискретные,нелинейные, оптимальные и адаптивные системы /С.В. Лукьянец, А.Т.Доманов,В.П.Кузнецов.М.А.Крупская-Мн.:БГУИР,2007. 5. Кузнецов А.П. Линейные импульсные системы: Математическое описание: Тексты лекций по курсу «Теория автоматического управления»б-Мн.:БГУИР,1996.-70с. |
;
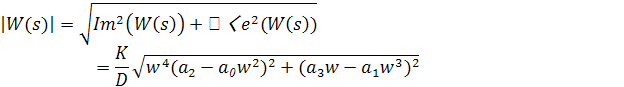
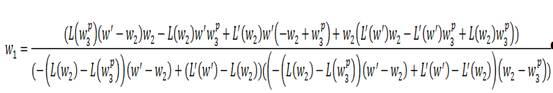
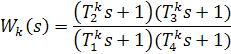
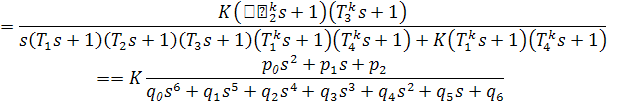
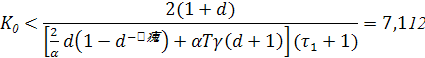
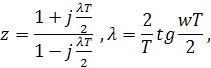
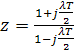при заданном значении
Т2, при котором система выходит на границу устойчивости.
(по условию)
0,03135
1,12127
5,223
=0,165
=с0
5,033
с0
)
передаточная функция системы по ошибке.
по графику
W(jw) находятся
частота искомого периодического (гармонического) режима w=w*, а
на прямой 
в точке
пересечения его амплитуда а = а*. Тогда в системе существуют периодические колебания:
находим а*=0.41.
пересечение АФЧХ W0(jw) происходит «изнутри наружу»,
то такой периодический режим будет устойчивым,
т.е. в системе существуют автоколебания с частотой w* и амплитудой а*
.