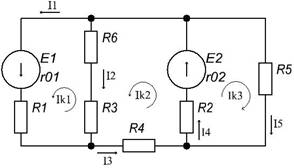
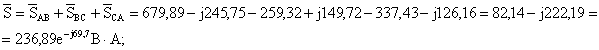Контрольная работа: Электрические цепи постоянного и переменного токаКонтрольная работа: Электрические цепи постоянного и переменного тока1. Анализ электрического состояния линейных и нелинейных электрических цепей постоянного тока 1.1 Расчет линейных электрических цепей постоянного тока Для электрической цепи, изображенной на (рис. 1.1), выполнить следующее: 1) составить на основании законов Кирхгофа систему уравнений для определения токов во всех ветвях схемы; 2) определить токи во всех ветвях схемы, используя метод контурных токов; 3) определить токи во всех ветвях схемы на основании метода наложения; 4) составить баланс мощностей для заданной схемы; 5) результаты расчета токов по пунктам 2 и 3 представить в виде таблицы и сравнить; 6) определить ток во второй ветви методом эквивалентного генератора; 7) построить потенциальную диаграмму для любого замкнутого контура, включающего обе ЭДС. Дано: E1=20 В, E2=30 В, R1=64 Ом, R2=43 Ом, R3=31 Ом, R4=25 Ом, R5=52 Ом, R6=14 Ом, r01=1 Ом, r02=2 Ом. Определить: I1 ,I2 ,I3 ,I4 ,I5.
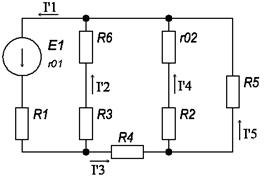
рис. 1.1 1) Составить систему уравнений, применяя законы Кирхгофа для определения токов во всех ветвях. Произвольно задаемся направлением токов в ветвях цепи I1,I2,I3,I4,I5. Составляем систему уравнений (в системе должно быть стока уравнений, скока в цепи ветвей). В нашей цепи пять ветвей, значит, в системе будет пять уравнений. Сначала составляем уравнение по первому закону Кирхгофа. В цепи с n узлами будет (n-1) уравнений, в нашей цепи три узла, значит, будет два уравнения. Составляем два уравнения, для двух произвольных узлов. узел D: I3=I1+I2 узел F: I4=I3+I5 Теперь составляем недостающие три уравнения для трех независимых контуров. Чтобы они были независимыми, надо в каждый контур включить хотя бы одну ветвь, не входящую в предыдущую. Задаемся обходам каждого контура и составляем уравнения по второму закону Кирхгофа. Контур ABCD – обход против часовой стрелки E1=I1(R1+r01)-I2(R3+R6) Контур CDFE – обход против часовой стрелки E2=I2(R3+R6)+I3R4+I4(R2+r02) Контур EGHF – обход по часовой стрелке E2=I4(R2+r02)+I5R5 ЭДС в контуре берется со знаком "+", если направление ЭДС совпадает с обходом контура, если не совпадает – знак "-". Падения напряжения на сопротивления контура, берется со знаком "+", если направления тока в нем совпадает с обходом контура со знаком "-", если не совпадает. Мы получили систему из пяти уравнений с пятью неизвестными:
Решив систему, определим величину и направление тока во всех ветвях схемы. Если при решении системы ток получается со знаком "-", значит его действительное направление обратно тому направлению, которым мы задались. 2) Определить токи во всех ветвях схемы, используя метод контурных токов. В заданной цепи можно рассмотреть три контура-ячейки (ABDC, CDFE, EGHF) и вести для них контурные токи Ik1, Ik2, Ik3. Контуры-ячейки имеют ветвь, не входящую в другие контуры – это внешние ветви. В этих ветвях контурные токи являются действительными токами ветвей. Ветви, принадлежащие двум смежным контурам, называются смежными ветвями. В них действительный ток равен алгебраической сумме контурных токов смежных контуров, с учетом их направления. При составлении уравнений по второму закону Кирхгофа в левой части равенства алгебраически суммируются ЭДС источников, входящих в контур-ячейку, в правой части равенства алгебраически суммируются напряжения на сопротивлениях, входящих в этот контур, а также учитывается падение напряжения на сопротивлениях смежной ветви, определяемое по контурному току соседнего контура. На основании вышеизложенного порядок расчета цепи методом контурных токов будет следующим: стрелками указываем выбранные направления контурных токов Ik1, Ik2, Ik3 в контурах-ячейках (направление обхода контуров принимаем таким же); составляем уравнения и решаем систему уравнений или методом подстановки, или с помощью определителей.
Подставляем численное значение ЭДС и сопротивлений:
или
Решим систему с помощью определителей. Вычислим определитель системы Δ и частные определители Δ1, Δ2, Δ3.
Вычислим контурные токи:
Вычислим действительные токи:
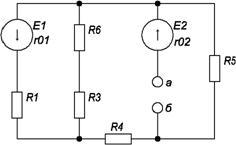
3) Определить токи во всех ветвях схемы на основании метода наложения. По методу наложения ток в любом участке цепи рассматривается как алгебраическая сумма частных токов, созданных каждой ЭДС в отдельности. а) Определить частные токи от ЭДС E1, при отсутствии ЭДС E2, т.е. рассчитать цепь по рисунку 1.2 Показываем направление частных токов от ЭДС E1 и обозначаем буквой I с одним штрихом (I'). Решаем задачу методом "свертывания".
рис 1.2
Ток источника:
Применяя закон Ома и первый закон Кирхгофа, вычисляем токи ветвей.
Токи ветвей:
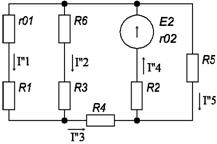
б) Определяем частные токи от ЭДС E2 при отсутствии ЭДС E1, т.е. рассчитываем простую цепь по рисунку 1.3. Показываем направление частных токов от ЭДС E2 и обозначаем их буквой I с двумя штрихами (I’’). Рассчитываем общее сопротивление цепи:
рис 1.3
Ток источника:
Применяя закон Ома и первый закон Кирхгофа, вычисляем токи ветвей:
Токи ветвей:
Вычисляем токи ветвей исходной цепи (рис 1.1), выполняя алгебраическое сложение токов, учитывая их направления:
Знак "-" говорит о том, что ток течет в обратном направлении которого мы задались в пункте а). 4) Составить баланс мощностей для заданной схемы. Источник E1 и E2 вырабатывают электрическую энергию, т.к. направление ЭДС и тока в ветвях с источниками совпадают. Баланс мощностей для заданной цепи пишется так: E1I1+E2I4=I12(R1+r01)+I22(R3+R6)+I32R4+I42(R2+r02)+I52R5. Подставляем числовые значения и вычисляем: 20ּ0,332+30ּ0,489=0,3322ּ65+0,0312ּ45+0,2992ּ25+0,4892ּ45+0,172ּ52 21,31Вт=21,706Вт С учетом погрешностей баланс мощностей получился. 5) Результаты расчетов токов по пунктам 2 и 3 представить в виде таблицы и сравнить.
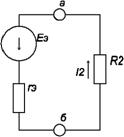
Расчет токов ветвей обоими методами с учетом ошибок вычислений примерно одинакова. 6) Определить ток во второй ветви методом эквивалентного генератора. Метод эквивалентного генератора используется для исследования работы какого-либо участка в сложной электрической цепи. Для решения задачи методом эквивалентного генератора разделим электрическую цепь на две части: потребитель (исследуемая ветвь с сопротивлением R2, в которой требуется определить величину тока) и эквивалентный генератор (оставшаяся часть цепи, которая для потребителя R2 служит источником электрической энергии, т. е. генератором). Получается схема замещения (рис. 1.4).
рис 1.4
рис 1.5 На схеме искомый ток I2 определим по закону Ома для замкнутой цепи:
Зная Ixx величины сопротивлений и ЭДС, в схеме можно определить Uxx как разность потенциалов между клеммами а и б. Для этого потенциал точки а будем считать известным и вычислим потенциал точки б. φб=φа+E2-IxxּR5 тогда Uxx=φб-φа=E2-IxxּR5=30-0,141ּ52=22,668В Для расчета внутреннего сопротивления эквивалентного генератора необходимо преобразовать активный двухполюсник в пассивный (рис. 1.6), при этом ЭДС Е1 и E2 из схемы исключается, а внутренние сопротивления этих источников r01 и r02 в схеме остаются. Вычисляем эквивалентное сопротивление схемы (рис 1.6) относительно зажимов а и б:
рис 1.6 Зная ЭДС и внутреннее сопротивление эквивалентного генератора, вычисляем ток в исследуемой ветви:
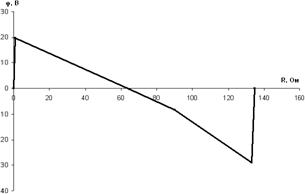
7) Построить потенциальную диаграмму для любого замкнутого контура, включающего обе ЭДС. Возьмем контур ABFE. Зададимся обходом контура против часовой стрелке. Заземлим одну из точек контура, пусть это будет точка А. Потенциал этой точки равен нулю, φA=0 (рис. 1.1). Зная величину и направление токов ветвей и ЭДС, а также величины сопротивлений, вычислим потенциалы всех точек контура при переходе от элемента к элементу. Начнем обход от точки А. φA’=φA+E1-I1r01=0+20-0,313ּ1=19,687 В φB=φA’-I1R1=19,687-0,313ּ64=-0,345 В φF=φB-I3R4= -0,345-0,32ּ25=-8,345 В φF’=φF-I4R2=-8,345-0,481ּ43=-29,028 В φE=φA=φF’+E2-I4r02= -29,028+30-0,481ּ2=0 В Строим потенциальную диаграмму. По оси абсцисс откладываем сопротивления контура в той последовательности, в которой производим обход контура, прикладывая сопротивления друг к другу, по оси ординат – потенциалы точек с учетом их знака.
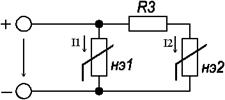
рис.1.7 1.2 Расчет нелинейных электрических цепей постоянного тока Построить входную вольтамперную характеристику схемы (рис. 1.8) Определить токи во всех ветвях схемы и напряжения на отдельных элементах, используя полученные вольтамперные характеристики. Использовать вольтамперные характеристики элементов "а" и "б" (рис 1.9). Дано: U=200 В. R3=32 Ом. нэ1=а нэ2=б Определить: I1, I2, I3, U1, U2, U3.
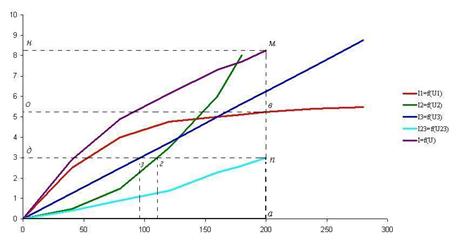
рис 1.8 Расчет цепи производим графическим методом. Для этого в обшей системе координат строим вольтамперные характеристики (ВАХ) линейного и нелинейных элементов: I1=f(U1), I2=f(U2), I3=f(U3) (рис 1.10).
рис 1.10 ВАХ линейного элемента
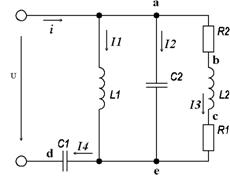
строим по уравнению Далее строится общую ВАХ цепи с учетом схемы соединения элементов. В нашей цепи соединение элементов смешанное. Поэтому графически "сворачиваем" цепь. Начнем с элемента I1=f(U1) (нэ1), он подсоединен параллельно цепи и его ВАХ будет таким же, как и при дано. Далее делаем характеристики линейного элемента I3=f(U3) и нелинейного элемента (нэ2) I2=f(U2), которые соединены между собой последовательно. Строим для них общую ВАХ. В данном случае задаемся током и складываем напряжения. Проделываем это многократно. По полученным точкам строим общую ВАХ цепи I23=f(U23). Затем строим ВАХ нелинейного элемента I1=f(U1) и I23=f(U23), они подсоединены в цепи параллельно, значит, их ток будет равен сумме токов I1=f(U1) и I23=f(U23), значит складываем на графике их общий ток I=f(U). Дальнейший расчет цепи производим по полученным графикам. Чтобы найти токи и напряжение на всех элементах цепи поступим так: по оси напряжение находим напряжение равное 200 В (точка а). Из этой точки восстанавливаем перпендикуляр до пересечения I1=f(U1), получаем точку "в". Из точки "в" опустим перпендикуляр на ось тока и получим точку "о", и получим ток (нэ1). Iнэ1=5,2А. Так же восстановим перпендикуляр из точки "а" до пересечение I23=f(U23) и опустим его на ось тока, получим ток во второй ветви I3,не2=I3=Iне2=3А. Отрезке "нд" пересекает ВАХ I3=f(U3) и I2=f(U2) в точках "з" и "г", опустим там перпендикуляры мы получим напряжение на элементах R3 (U3=95В) и (нэ2) (Uнэ2=105В). 2. Анализ электрического состояния линейных электрических цепей переменного тока: однофазных, трехфазных. Исследование переходных процессов в электрических цепях 2.1 Расчет однофазных линейных электрических цепей переменного тока К зажимам электрической цепи (рис 2.1), подключен синусоидальное напряжение u=54sin(ωt+60º) В частотой f=50Гц. Выполнить следующее: 1) определить реактивное сопротивление элементов цепи; 2) определить действующие значения токов во всех ветвях цепи; 3) записать уравнение мгновенного значения тока источника; 4) составить баланс активных и реактивных мощностей; 5) построить векторную диаграмму токов, совместимую с топографической векторной диаграммой напряжений. Дано: R1=10 Ом; R2=20 Ом; L1=31,8 мГн; L2=50,9 мГн; C1=318 мкФ; C2=199 мкФ. Определить: XL1, XL2, XC1, XC2, I, I1, I2, I3, I4, i.
рис 2.1 1) Реактивное сопротивление элементов цепи.
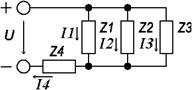
2) Расчет токов в ветвях цепи выполнен методом эквивалентных преобразований. Представим схему, приведенную на рисунке 2.1, в виде:
рис 2.2 Находим комплексные сопротивления ветвей, затем участков цепи и всей цепи:
Выразим действительное значение напряжение в комплексной форме:
Вычисляем общий ток цепи:
Для определения токов параллельных ветвей I1, I2, I3, рассчитываем напряжение на зажимах:
Вычисляем токи ветвей:
3) Уравнение мгновенного значения тока источника:
4) Составить баланс активных и реактивных мощностей:
где Sист=150,488 ВּА, Pист=122,96 Вт, Qист= -86,74 вар. Активная Pпр и реактивная Qпр мощность приемников: Pпр=I32(R1+R2)=2,032ּ30=123,62 Вт; Qпр=I12(XL1)+I22(-XC2)+I32(XL2)+I42(-XC1)=6,892ּ10+4,32ּ(-16)+2,032ּ16+3,962ּ(-10)=-88вар Баланс мощностей выполняется: Pист=Pпр, Qист=Qпр 123Вт=124Вт, -87вар=-88вар. Баланс мощностей практически сходится. 5) Напряжения на элементах:
6) Строим топографическую векторную диаграмму на комплексной плоскости. Выбираем масштаб: MI=1 А/см, MU=10 В/см. Определяем длины векторов токов и напряжений:
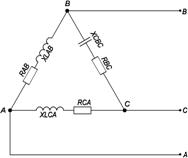
рис 2.3 На комплексной плоскости в масштабе откладываем векторы токов в соответствии с расчетными значениями, при этом положительные фазовые углы отсчитываем от оси (+1) против часовой стрелке, а отрицательные - по часовой стрелке. Топографическая векторная диаграмма напряжений характерна тем, что каждой точке диаграммы соответствует определенная точка электрической цепи. Построение векторов напряжений ведем, соблюдая порядок расположения элементов цепи и ориентируя векторы напряжений относительно векторов тока: на активном сопротивлении ток и напряжение совпадают по фазе, на индуктивном элементе напряжение опережает ток на 90°, а на емкостном напряжение отстает от тока на 90°. 2.2 Расчет трехфазной линейной цепи переменного тока В цепи, изображенной на схеме (рис. 2.4), потребители соединены треугольником. Известно линейное напряжение Uл=38 В и сопротивление фаз. RAB=18,8 Ом; RBC=3,8 Ом; RCA=3,1 Ом; XLAB=0,68 Ом; XLAC=2,57 Ом; XCBC=2,2 Ом. Определить фазные, линейные токи, мощности активные, реактивные, полные мощности каждой фазы и всей цепи. Построить векторную диаграмму цепи. Дано: Uл=38 В; RAB=18,8 Ом; RCA=3,1 Ом; XLAB=0,68 Ом; XLCA=2,57 Ом; XCBC=2,2 Ом. Определить: IA, IB, IC, IAB, IBC, ICA, P, Q, S.
рис 2.4 При соединении трехфазной цепи треугольником расчет будет вести символическим методом. 1) Модули фазных напряжений при соединении треугольником равны линейным напряжениям. UЛ=UФ=38 В, то есть Комплексы данных
напряжений запишем из условия, что вектор
2) Вычислить комплексы фазных сопротивлений.
где ZAB=2 Ом, φAB=19,9º;
где ZBC=4,82 Ом, φBC=30º;
где ZCA=4,03 Ом, φCA=39,5º. 3) Определить фазные токи:
модуль IAB=19 А, ψAB=-19,9º;
модуль IBC=7,88 А, ψBC=-90º;
модуль ICA=9,43 А, ψCA=80,5º. 4) Находим линейные токи из уравнений, записанных по первому закону Кирхгофа для узлов A, B, C.
модуль IА=22,69 А, аргумент ψА=44º;
модуль IB=17,93 А, аргумент ψB=-4,5º;
модуль IC=17,25 А, аргумент ψC=84,9º. 5) Вычислить мощность каждой фазы и всей цепи:
где SAB=722 BּA, PAB=679,89 Вт, QAB=-245,75 вар;
где SВС=299,44 BּA, PBС=-259,32 Вт, QAB=149,72 вар;
где SCA=360,24 BּA, PCA=-337,43 Вт, QAB=-126,16 вар;
где S=236,89 BּA, P=82,14 Вт, QAB=-222,19 вар. 6) Строим в масштабе векторную диаграмму напряжений и токов. Векторы фазных токов
Замыкающие векторные
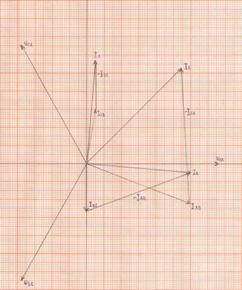
треугольники векторов Выбираем масштаб: MI=3 А/см.
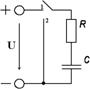
рис 2.5 2.3 Исследование переходных процессов в электрических цепях, содержащих конденсатор и сопротивление Цепь с последовательно включенными конденсатором емкостью С = 50 мкФ и сопротивлением R = 10 КОм подсоединяется к источнику постоянного напряжения U = 50 В (переключатель в положении 1). Определить законы изменения переходных напряжений и тока при заряде конденсатора и построить их графики. Затем цепь отключается от источника и одновременно переключатель переводится в положение 2. Определить законы изменения переходных напряжений и тока при разряде конденсатора и построить их графики. Определить фактическую длительность заряда и разряда конденсатора и энергию электрического поля при 1 = Зτ. Схема цепи приведена на рис. 2.6. Дано: С = 50 мкФ, R = 10 КОм, U = 50 В. Определить: i=f(t),t; uc=f(t),W.
рис 2.6 1) Переключатель в положении 1 (заряд конденсатора) τ =RּC=104ּ50ּ16-6=0,5c На основании второго закона коммутации получены законы, характеризующие напряжение и ток при заряде конденсатора.
где U – напряжение источника uуст=U – установившееся значение напряжения при заряде конденсатора
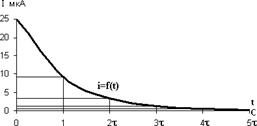
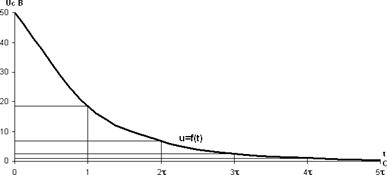
Зарядный ток равен свободной составляющей, т.к. ток установившегося режима равен 0(iуст=0). Длительность заряда конденсатора: t=5τ=5ּ0,5=2,5 с. Вычисляем значение напряжения на конденсаторе при его заряде для значений времени t=0, τ, 2τ, 3τ, 4τ, 5τ. t=0, t=τ, t=2τ, t=3τ, t=4τ, t=5τ, Аналогично вычисляем значения зарядного тока согласно закону изменения переходного тока при заряде конденсатора для значений времени t=0, τ, 2τ, 3τ, 4τ, 5τ.
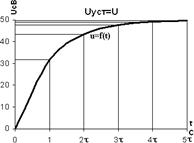
Согласно полученным результатам строим графики зарядного напряжения и тока в зависимости от τ. (рис 2.7)
рис 2.7 Из построенных графиков u(t) и i(t) можно для любого момента времени определить значение u и i, а также рассчитать запасенную энергию в электрическом поле заряженного конденсатора. Например, при t=3τ:
2) Переключатель в положении 2 (разряд конденсатора). Быстрота разряда конденсатора также зависит от параметров цепи и характеризуется постоянной времени, разряда конденсатора: τ =RC=104ּ50ּ10-6=0,5 с На основании второго закона коммутации получены законы, характеризующие напряжение и ток при разряде конденсатора:
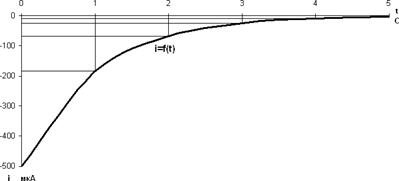
где U – напряжение заряженного конденсатора до начала разряда. Разрядные напряжения и ток равны их свободным составляющим, т.к. напряжение и ток установившегося режима после разряда равны 0 (uc уст=0, iуст=0). Длительность разряда конденсатора: t=5τ=0,5ּ5=2,5 с. Вычисляем значения напряжения конденсатора при его разряде для, значений времени t=0, τ, 2τ, 3τ, 4τ, 5τ. t=0, t=τ, t=2τ, t=3τ, t=4τ, t=5τ, Аналогично вычисляем значения разрядного тока согласно закону изменения переходного тока при разряде конденсатора для тех же значений времени.
Знак "-" говорит о том, что разрядный ток имеет обратное направление зарядному. t=0, t=τ, t=2τ, t=3τ, t=4τ, t=5τ, Согласно полученным расчетам строим графики разрядного напряжения и тока в зависимости от τ (рис 2.8).
рис 2.8 Энергия электрического поля конденсатора в момент времени t=3τ:
Литература 1 Галицкая Л.Н. "Теоретические основы электротехники. Курсовое проектирование" – Минск 1997г. 2 Попов В.С. "Теоретическая электротехника" - Москва 1990г. 3 Евдокимов Ф.Е. "Теоретические основы электротехники". Издательство "Высшая школа" - Москва 2002г. 4 Вычисляем токи ветвей исходной цепи, выполняя алгебраическое сложение частных токов, учитывая их направления. |
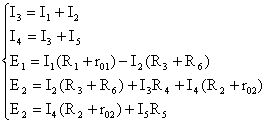 .
.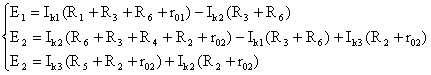 .
.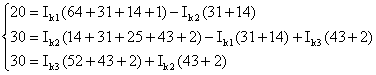
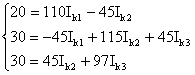
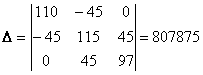 ;
; 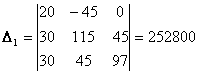 ;
;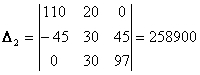 ;
; 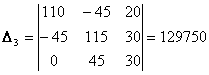 .
.
 Ом
Ом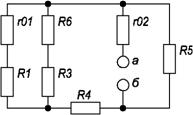
 А.
А. А;
А; А;
А; А.
А.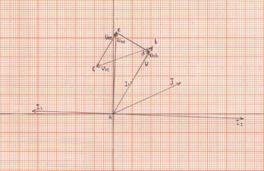
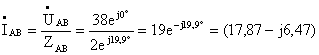 А,
А, ,
, А,
А,