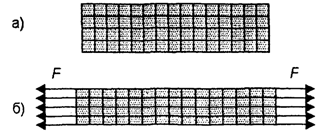
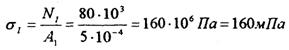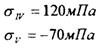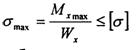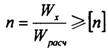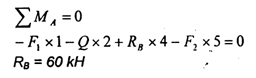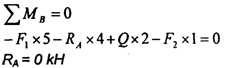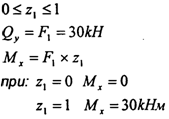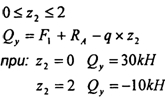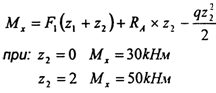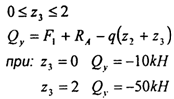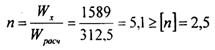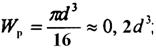Контрольная работа: Сопротивление материаловКонтрольная работа: Сопротивление материаловСОПРОТИВЛЕНИЕ МАТЕРИАЛОВ ВВЕДЕНИЕ При проектировании различных конструкций необходимо производить расчёты на прочность. Неправильный расчёт самой на первый взгляд незначительной детали может повлечь за собой очень тяжёлые последствия, привести к разрушению всей конструкции. Кроме расчётов на прочность, во многих случаях проектирования производят расчёты на жёсткость и устойчивость. Данное методическое указание посвящено только вопросам расчётов на прочность при различных нагрузках и видах деформации. ОПРЕДЕЛЕНИЕ НАПРЯЖЕНИЙ ПРИ РАСТЯЖЕНИИ (СЖАТИИ) ОСНОВНЫЕ ПОНЯТИЯ При растяжении (сжатии) бруса в его поперечных сечениях возникают только нормальные напряжения. Гипотеза плоских сечений Я. Бернулли: сечения бруса, плоские и нормальные к его оси до деформации, остаются плоскими и нормальными к оси и при деформации.
При растяжении (сжатии) бруса нормальные напряжения распределены по его поперечному сечению равномерно.
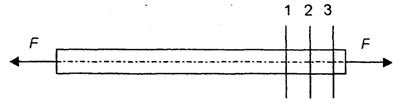
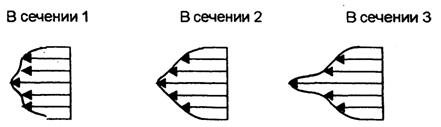
- нормальное напряжение, возникающее в материале при растяжении (сжатии), А - площадь поперечного сечения, N - сила вызывающая деформацию. Для нормальных напряжений принимают то же правило знаков, что и для продольных сил, т.е. при растяжении считают напряжения положительными. Принцип Сен-Венана: Распределение напряжений существенно зависит от способа нагружения внешних сил лишь в близи места нагружения. В частях, достаточно удалённых от места приложения сил, распределение напряжений практически зависит только от статического эквивалента этих сил, а не от способа их приложения.
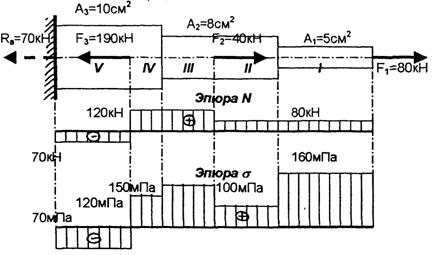
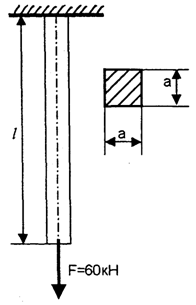
В тех случаях, когда нормальные напряжения в различных поперечных сечениях бруса неодинаковы, целесообразно показывать закон их изменения по длине бруса в виде графика — эпюры нормальных напряжений ПРИМЕР РЕШЕНИЯ ЗАДАЧ Для бруса со ступенчато-переменным поперечным сечением построить эпюры продольных сил и нормальных напряжений:
Решение: Разбиваем брус на участки, начиная от свободного конца. Границами участков являются места приложения внешних сил и изменения размеров поперечного сечения, т.е. брус имеет пять участков. При построении эпюры N достаточно было разбить брус только на три участка в местах приложения сил. Нормальные напряжения вычисляем по формуле: σ = N/А
Аналогично:
В пределах каждого из участков напряжения постоянны, т.е. эпюра на данном участке — прямая, параллельная оси Х. Для расчётов на прочность интерес представляют в первую очередь те сечения, в которых возникают наибольшие напряжения. Интересно также отметить, что максимальные напряжения, возникающие в исследуемом образце, не всегда совпадают с максимальными продольными силами. ОПРЕДЕЛЕНИЕ ДЕФОРМАЦИЙ ПРИ РАСТЯЖЕНИИ (СЖАТИИ) ОСНОВНЫЕ ПОНЯТИЯ Продольная деформация (относительное удлинение) - отношение приращения (изменения) длины элемента к его первоначальной длине.
Тоже самое можно сказать
и о поперечной деформации: В известных пределах нагружения между упругой продольной деформацией и соответствующим (действующим в её направлении) нормальным напряжением существует прямо пропорциональная (линейная) зависимость: σ=E*ε , где Е - модуль упругости (модуль Юнга), Па, мПа, физическая постоянная данного материала, характеризующая его жёсткость (табличное значение). Так как: σ = N/A то получим формулу Гука: Δl=N·l/(Е·А), где:Δl - изменение длины всего объекта; l - первичная длина объекта. Отсюда: С = Е А/l- жёсткость бруса; β=l/С = l/(Е . А) - коэффициент податливости. Следовательно: Δl=N/С Δl=βN [ ]—допускаемое значение. ПРИМЕР РЕШЕНИЯ ЗАДАЧ Определить размеры поперечного сечения стальной (Е=2,1 1О5мПа) штанги (длина l= 2,5м) при условии, чтобы её удлинение равнялось [Δl]= 2мм. Чему при этом будут равны напряжения в поперечном сечении штанги?
Решение: По формуле Гука, учитывая, что продольная сила во всех поперечных сечениях штанги одинакова (N=F), имеем:
Найдем площадь поперечного сечения штанги при Δl=[Δl]=2мм:
А напряжение в поперечном сечении штанги будет равно:
Примечание: изменение площади поперечного сечения ничтожно мало, поэтому при расчетах напряжений всегда оперируют первоначальной площадью поперечного сечения. РАСЧЁТЫ НА ПРОЧНОСТЬ ПРИ РАСТЯЖЕНИИ (СЖАТИИ) ОСНОВНЫЕ ПОНЯТИЯ Условие прочности:
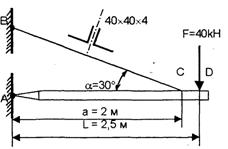
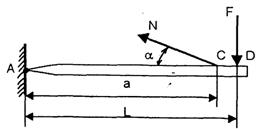
где: n — коэффициент запаса прочности должно соблюдаться для всех точек рассматриваемого элемента конструкции, поэтому под σ следует понимать наибольшее расчетное напряжение. Примечание: незначительное превышение наибольших расчетных напряжений над допускаемыми, конечно, не опасно, так как допускаемое напряжение составляет лишь некоторую часть от предельного. Считается, что это превышение может достигать 3% от допускаемого напряжения. Если расчетное напряжение значительно ниже допускаемого, это является свидетельством нерациональности конструкции, перерасхода материала. В зависимости от цели расчета (постановки задачи) различают три вида расчетов на прочность: - проверочный; - проектный; - определение допускаемой нагрузки. При проверочном расчете известны: нагрузка элемента конструкции, его материал (а следовательно, допускаемое или предельное напряжение), размеры. Определению подлежит наибольшее расчетное напряжение, которое сравнивают с допускаемым. С подобными расчетами встречаются, в частности, при экспертизе выполненных проектов. При проектном расчете известны нагрузки и материал (допускаемые напряжения). Определению подлежит требуемая площадь поперечного сечения расчетного элемента конструкции. В некоторых случаях проверочный расчет удобнее вести в форме определения допускаемой нагрузки. Это целесообразно при изменении режимов тех или иных технологических процессов, когда возникает необходимость в повышении нагрузок существующего оборудования и, следовательно, надо знать их предельно допускаемое по условию прочности значение. ПРИМЕР РЕШЕНИЯ ЗАДАЧ Проверить прочность тяги ВС. Материал — сталь Ст 3, допускаемое напряжение [σ]= 16ОмПа.
Решение:
Откуда:
Напряжения в поперечном сечении тяги:
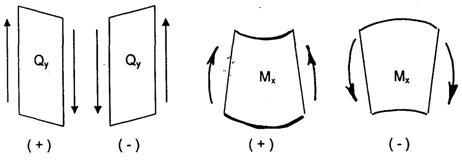
где: площадь поперечного сечения одного равнобокого уголка 40×40×4, А1 = 3,08 см2 (по табл. ГОСТ 8509-86). Площадь сечения тяги А = 2А1. Напряжение выше допускаемого всего на 1,25%, следовательно, прочность тяги обеспечена. РАСЧЁТЫ НА ПРОЧНОСТЬ ПРИ ИЗГИБЕ ОСНОВНЫЕ ПОНЯТИЯ Изгиб – это такой вид деформации бруса, при котором в его поперечных сечениях возникают изгибающие моменты. При изгибе в поперечных сечениях бруса (балки) возникают два внутренних силовых фактора: поперечная сила и изгибающий момент Мх. Поперечная сила СЬ, в произвольном поперечном сечении бруса численно равна алгебраической сумме внешних сил, приложенных к его отсечённой части. Изгибающий момент М в произвольном поперечном сечении бруса численно равен алгебраической сумме моментов всех внешних сил, приложенных к отсечённой части, относительно той точки продольной оси бруса, через которую проходит рассматриваемое сечение. ПРАВИЛА ЗНАКОВ Поперечные силы считаются положительными, если они стремятся повернуть элемент бруса по часовой стрелке. Изгибающий момент считается положительным, если элемент бруса изгибается выпуклостью вниз, т.е. таким образом, что его сжатые волокна находятся в верхней части.
УСЛОВИЕ ПРОЧНОСТИ
либо:
где: Мх мах , — максимальный изгибающий момент (в самом опасном сечении); Wх — момент сопротивления сечения, выражается в см3, табличная величина. КОЭФФИЦИЕНТ ЗАПАСА
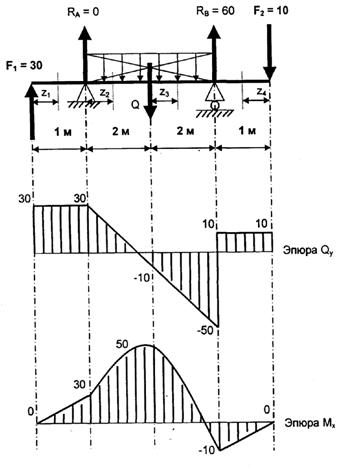
для Стали З (ГОСТ 380-94) [n] = 2,5 Моменты сопротивления сечения круга, кольца, прямоугольника находим по следующим формулам: круг: кольцо: где: с – ширина кольца прямоугольник: ПРИМЕР РЕШЕНИЯ ЗАДАЧ Проверить прочность стальной балки (Сталь З [σ] = 160 МПа). Поперечное сечение балки — двутавр № 50(Wх = 1589 см3) действующие силы: q = 20 кН; F= 30 кН; F=10кН.
Решение:
при: z3=0 Мх=5ОкНм z3=2 Мх=-10кНм 0≤z4≤1 Qy=F2=10kН Мx= -F2 ×z4 при: z4 =0 Мx =0 z4=1 Мx=-10kНм Согласно полученным значениям строим эпюры изгибающих сил и изгибающих моментов. Обязательно учитываем, что изгиб параболы области распределённой нагрузки, должен быть направлен навстречу линиям действия распределённой нагрузки. Определяем по эпюре изгибающих моментов пик — Мx — максимальный изгибающий момент и производим расчёт на прочность:
Допустимый коэффициент запаса для Стали З — [n]=2, 5. Следовательно:
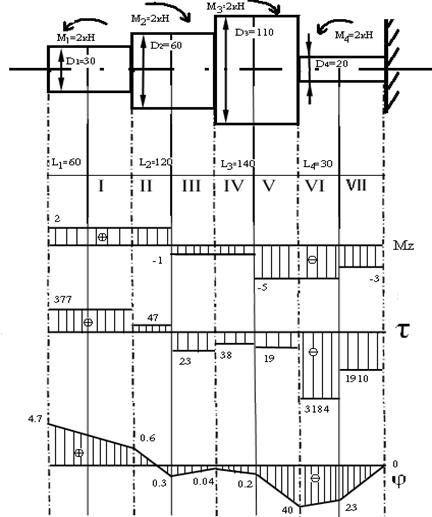
Условие прочности выполняется. РАСЧЕТЫ НА ПРОЧНОСТЬ ПРИ КРУЧЕНИИ ОСНОВНЫЕ ПОНЯТИЯ Кручение – это такой вид деформации бруса, при котором в его поперечных сечениях возникает единственный внутренний силовой фактор – крутящий момент Мz. τ=Mz/Wp – касательное напряжение где: Mz – крутящий момент Wp – полярный момент сопротивления сечения φ=Mz/(G*Wp)=[радианы] – угол поворота сечения где: G – постоянная характеризующая материал (СТАЛЬ 3 G=8*1010Па=80*104мПа) круг: Кольцо: ПРИМЕР РЕШЕНИЯ ЗАДАЧ
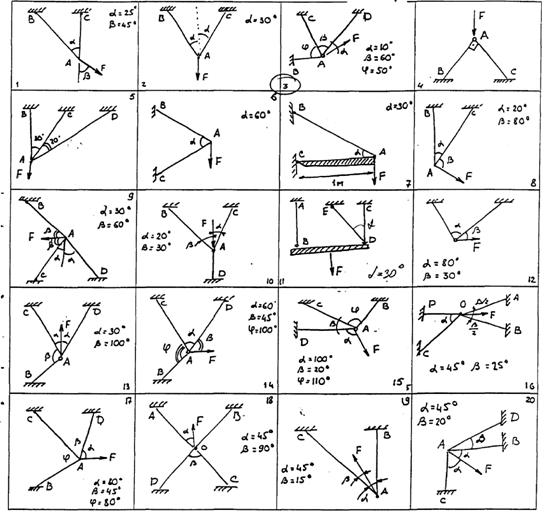
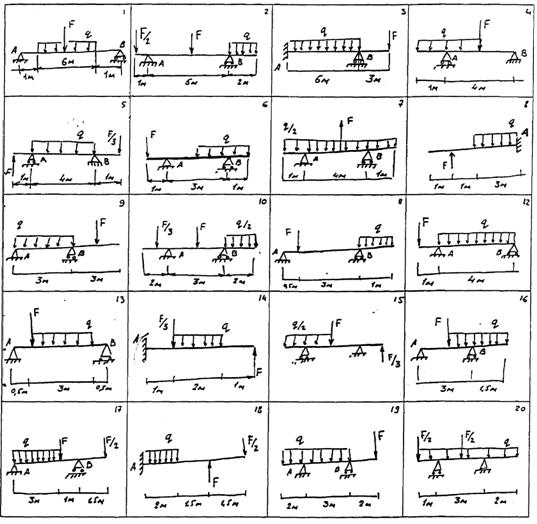
W1=πD1/16 => τ1=Mz*16/(π*D13)=2.0*103/(3.12*0.033)=377*106 Па=377мПа τ2=2*103*16/(π*D23)=47мПа τ3=-1*103*16/(π*D23)=-23мПа τ4=-1*103*16/(π*D33)=-3,8мПа τ5=-5*103*16/(π*D33)=-19мПа τ6=-5*103*16/(π*D43)=-3184мПа τ7=-1910мПА φ=M/(G*W)=M*16/(G*π*D3)=τ/G φ1=377*(8*106)=47*10-3 рад φ2=-0,6*10-3 рад φ3=-0,3*10-3 рад φ4=-0,04*10-3 рад φ5=-0,2*10-3 рад φ6=-40*10-3 рад φ7=-23*10-3 рад Требования к содержанию и оформлению расчетно-графических работ Цель расчетно-графических работ - закрепить знания входящие в курс "Сопротивление материалов", привить навыки работы с научной литературой. В процессе выполнения расчетно-графических работ студент применяет все знания по механике, которые получил ранее и получает навыки инженерного мышления. Основная задача расчетно-графической работы № 1 — решение двух задач: 1. Задача по разделу сопротивления материалов «Растяжение, сжатие». 2. Задача по разделу сопротивления материалов «Растяжение, сжатие». Основная задача расчетно-графической работы № 2 — решение трёх задач: 3. Задача по разделу сопротивления материалов «Изгиб». 4. Задача по разделу сопротивления материалов «Изгиб». 5. Задача по разделу сопротивления материалов «Кручение». Расчетно-графические работы предусмотрены в объеме 5-10 рукописных листов пояснительной и расчетной записки и 1 листа формата А3 графической части, на которой изображаются все расчетные схемы к задачам с указанием направления действия сил и т.д. (желательно в цветном исполнении). РГР № 1 Задача №1 Определить допускаемую силу F. Стержни изготовлены из дюралевых труб одинакового сечения. Допускаемое напряжение [σ]=75МПа
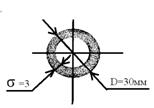
Задача №2 Проверить прочность стержней, если они нагружены силой F=40kH. Стержни изготовлены из дюраля одинакового сечения D=25мм. Допускаемое напряжение [σ]=75МПа. Условия соответствуют рисункам задачи №1. Варианты: 1-20 РГР № 2 Задача №1 Проверить прочность и жесткость стальной балки если [σ]=160МПа Поперечное сечение балки – двутавр №50 Wх=1589см3 Действующие силы q=20kN/m; F=30kN.
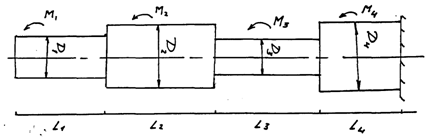
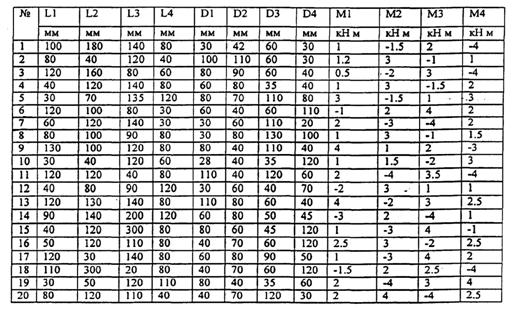
Задача №2 Условие данной задачи соответствует условию задачи №3 + 3 (после 20-го варианта идёт повторение, например: вариант 19 + 3 = 2 ватиант). Варианты: 1-20 Задача№3 Ступенчатый стальной брус круглого поперечного сечения жестко заделан одним концом и нагружен. как показано на рисунке. Построить эпюры крутящих моментов. максимальных касательных напряжений и углов поворотов поперечных сечений. Проверить прочность бруса при [τk] – 60Мпа.
Список используемой литературы: 1. А.А. Яблонский Курс теоретической механики часть 2. 2. Прикладная механика и механика «методические указания и контрольные задания 3. Айзенбуерг Т.Б., Воронков И.М., Осецкий В.М. Руководство к решению задач по теоретической механике. 4. Воронков И.М. Курс теоретической механики. 5. Добронравов В.В., Никитин Н.Н., Дворников А.А. Курс теоретической механики 6. Мещерский И.В. Сборник задач по теоретической механике. 7. Основы теоретической механики. В.Я. Молотников, Высшее образование, 2004г 8. Сопротивление материалов. Г.М. Ицкович. Высшая школа, 1998г. 9. Конструирование узлов и деталей машин. Высшая школа. П.Ф. Данаев, О.П. Леликов. 10. детали машин. М.Н. Иванов; Москва; Высшая школа, 1984г. 11. Справочник конструктора-машиностроителя. В.И. Анурьев 1,2Зт. Приложение: Ниже приведена таблица, по которой учащийся, зная свой вариант, сможет определить тот ряд задач, который ему предстоит решить (номер варианта определяется исключительно по согласованию с преподавателем).
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||