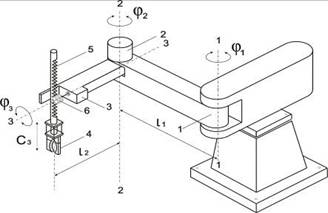
Курсовая работа: Проектирование управляемого привода в электромеханических системахКурсовая работа: Проектирование управляемого привода в электромеханических системахПОЯСНИТЕЛЬНАЯ ЗАПИСКА Тема: "Проектирование управляемого привода в электромеханических системах" Техническое задание на проектирование управляемого электропривода 1. Конструктивная схема (рис. 1) промышленного робота (ПР) с грузоподъемностью от 10 до 30 кг, используемого в сборочных операциях в автомобильной промышленности. ПР – автоматическая стационарная машина, имеющая исполнительный механизм (манипулятор) с тремя степенями подвижности. Два механизма поворота, расположенные в шарнирах 1 и 2, осуществляют программные повороты j1(t), j2(t) вокруг вертикальных осей (1–1 и 2–2 соответственно), механизм подъема 3 осуществляет поступательное перемещение С3(t) объекта манипулирования, зажатого в захватывающем механизме 4. В механизме подъема 3 использована зубчато-реечная передача с зубчатой рейкой 5 и зубчатой шестерней 6.
Рис. 1. Конструктивная схема промышленного робота 2. Перемещения по степеням подвижности осуществляются последовательно, начиная с перемещения j1(t). 3. Силовой модуль первого из индивидуальных приводов промышленного робота (рисунок 1) сосредоточен в центре масс шарнира 1. Центр тяжести груза (объекта манипулирования) совпадает с центром приведения масс захватывающего механизма 4. 4. Для данного ТЗ управляемый привод по координате j1(t) – программный, типа «угол – угол». 5. Описание и параметры программных траекторий рабочих циклов исследуемого привода приведены на рисунках 2 и 3.
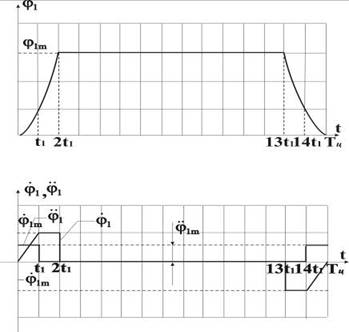
Рис. 2. Первая из двух возможных траекторий рабочего цикла для первого привода
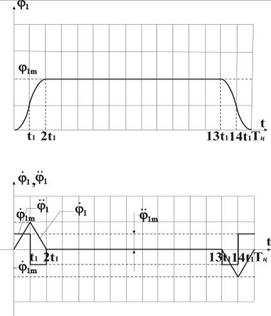
Рис. 3. Вторая из двух возможных траекторий рабочего цикла для первого привода
6. Масса зубчатой рейки mp = 5 кг, минимальное mmin = 15,5 кг и максимальное mmax= 25 кг значения массы груза вместе с массой захватывающего механизма. 7. Длина звеньев манипулятора l1= 0,5 м и l2 = 0,5 м (рис. 1). 8. Массы звеньев m1 = 54 кг и m2 = 4 кг. 9. Расстояние от центров масс звеньев до соответствующих шарниров r1 = 0,25 м и r2 = 0,25 м. 10. Динамические моменты инерции J1 = 0,3 кг.м2 и J2= 0,25 кг.м2 первого и второго звеньев относительно вертикальных осей, проходящих через их центры масс. Максимальный J3max = 0,3 кг.м2 и минимальный J3min= 0,15 кг.м2 динамические моменты инерции третьего звена: зубчатой рейки с захватывающим механизмом и грузом. 11. Коэффициент вязкого трения Квт = 0,04. 12. Момент сухого трения Мо = 0,05 Н.м. 13. КПД редуктора h = 0,65. 14. Передаточное отношение зубчато-реечной передачи iрп. 15. Параметры усилителя мощности kу = 220, Tm = 0,0015 с. 16. Статическая ecт = 1,0% и динамическая eд = 0,9% допустимые погрешности привода. 17. Прямые показатели качества: перерегулирование s = 25% и время переходного процесса tпп = 1,5 c. Управляемый электропривод получил широкое применение во всех сферах жизни и деятельности общества от промышленного производства до бытовой техники. Широта применения определяет исключительно большой диапазон мощностей электроприводов и значительное разнообразие их исполнения. В управляемом электроприводе нашли применение и получили развитие основные достижения современной техники управления. В ходе выполнения курсовой работы необходимо разработать конкретный электропривод, программно управляющий угловым перемещением промышленного робота-манипулятора по одной из трех степеней подвижности. Для наглядности корректности функционирования синтезированного управляемого электропривода выполнение работы включает построение его цифровой модели и оценку ее качественных показателей, используя средства компьютерного моделирования. 1 Энергетический расчет привода 1.1 Определение заданных программных траекторийОпределим постоянную времени
Приведем максимально возможное значение угловой координаты перемещаемой нагрузки к размерности [рад].
Рассчитаем неопределенные параметры для первой возможной траектории движения рабочей нагрузки за время одного цикла работы двигателя. Таблица 1.1
Для нахождения параметров траектории решим систему уравнений (1.3), приравняв значения угла поворота и скорости нагрузки в общих для сопряженных участках точках.
Из второго уравнения системы (1.3) получим зависимость для параметра b и подставим его в первое выражение.
Получим численные значения параметров a и b.
По формуле 1.5 найдем параметры a и b:
Таблица 1.2
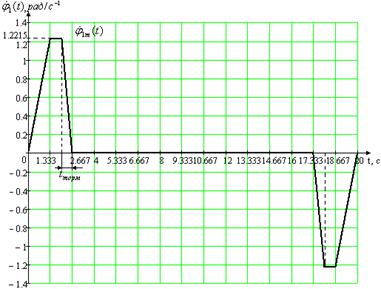
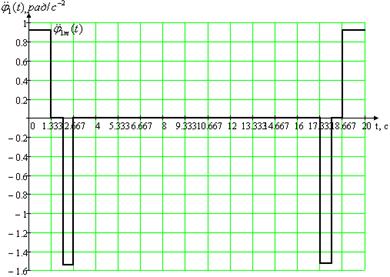
Максимальные значения: а) угла поворота нагрузки 1m(t) = 2.443 рад, б) угловой скорости нагрузки p1m(t) = 1.2215 рад/c-1, в) углового ускорения нагрузки p21m(t) = 0.916 рад/c-2. Рассчитаем неопределенные параметры для второй возможной траектории движения рабочей нагрузки за время одного цикла работы двигателя. Таблица 1.3
Для нахождения параметров траектории решим систему уравнений (1.6), приравняв значения угла поворота и скорости нагрузки в общих для сопряженных участках точках.
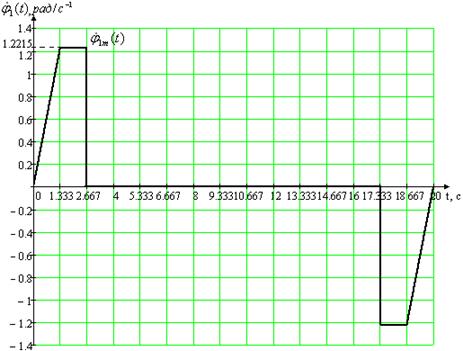
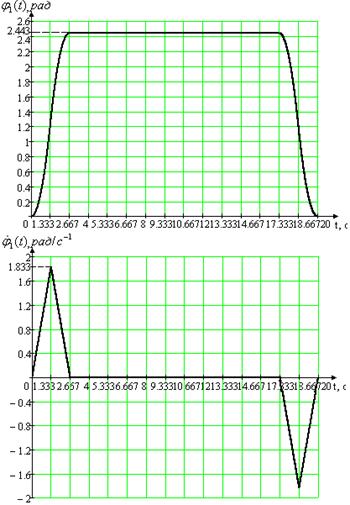
Рис. 1.1. Первая из двух возможных траекторий рабочего цикла для первого привода Из первого уравнения системы (1.8) получим формулу для параметра b и подставим его в третье выражение, а затем функциональные зависимости для параметров a и b – во второе уравнение
Получим численные значения параметров a, b и :
Таблица 1.4
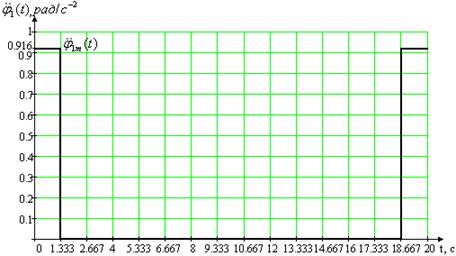
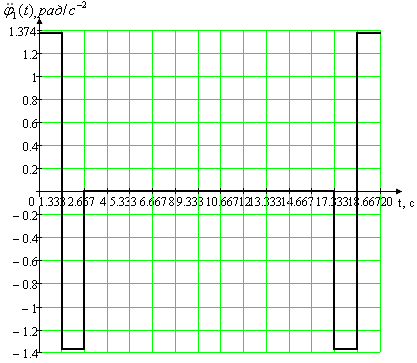
Максимальные значения: а) угла поворота нагрузки 1m(t) = 2.443 рад, б) угловой скорости нагрузки p1m(t) = 1.833 рад/c-1, в) углового ускорения нагрузки p21m(t) = 1.374 рад/c-2.
Рис. 1.2. Вторая из двух возможных траекторий рабочего цикла для первого привода 1.2 Расчет статической и динамической нагрузки на проектируемый привод
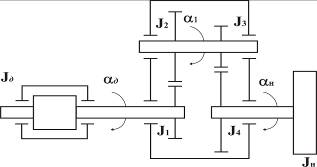
Рис. 1.3. Многомассовая нагрузка привода При определении энергетических параметров
проектируемого привода сложную многомассовую нагрузку привода (рис. 1.3) приводят
к одному валу – валу двигателя. Для этого многомассовую нагрузку с мощностью
где С другой стороны,
где
откуда:
где Моменты, действующие на валу нагрузки, можно
разделить на две группы. К первой группе относятся динамические моменты Таким образом, момент нагрузки, приведенный к валу двигателя,
Динамические моменты нагрузки приводов Динамический момент нагрузки первого привода определяется уравнением
где Нагрузка первого привода является телом сложной
конфигурации, поэтому
Динамический момент инерции третьего звено J3 принимает значения в диапазоне от J3 min до J3 max. Масса груза, зажатого в захватном устройстве m, может меняться в пределах от mmin до mmax. Изменение данных параметров приводит к изменению момента инерции нагрузки J. Определим минимальное и максимальное значение момента инерции нагрузки J:
Наибольшего значения величина динамического момента нагрузки привода достигает при максимальном угловом ускорении рабочей нагрузки
Определим максимальный динамический момент нагрузки привода для первой возможной траектории рабочего цикла первого привода по формуле 1.16.
Определим максимальный динамический момент нагрузки привода для второй возможной траектории рабочего цикла первого привода:
Статические моменты нагрузки приводов Движению в механизмах поворота противодействуют статические моменты сопротивления: моменты вязкого и сухого трения, характерные для зубчатых передач механизмов поворота. Момент вязкого трения пропорционален угловой скорости вала нагрузки и определяется уравнением:
где Момент сухого трения в большинстве случаев считают независимым от скорости и направленным против нее:
здесь Согласно (1.17), (1.18), статический момент нагрузки первого привода
а его максимальное значение
По формуле 1.20 найдем максимальный статический момент нагрузки привода для первой возможной траектории рабочего цикла:
По формуле 1.20 найдем максимальный статический момент нагрузки привода для второй возможной траектории рабочего цикла:
1.3 Предварительный выбор двигателяИсходными данными для выбора двигателя являются
приведенный к валу двигателя момент рабочей нагрузки Выбор исполнительного двигателя начнем с
расчета требуемой максимальной мощности Для первого привода, осуществляющего поворот
По формуле 1.21 вычислим требуемую мощность двигателя для отработки первой из двух возможных траекторий движения рабочей нагрузки:
По формуле 1.21 вычислим требуемую мощность двигателя для отработки второй из двух возможных траекторий движения рабочей нагрузки
Выберем исполнительный двигатель с номинальной
мощностью не меньшей Выбор будем осуществлять согласно следующим критериям: 1. 2. 3. 4. 5. 6.
Согласно (1.22), для первой траектории будем
выбирать двигатель, придерживаясь данных значений мощности: Для обеспечения движения рабочей нагрузки по первой из двух рассматриваемых траекторий наиболее подходящими приводами являются двигатели [1], приведенные в таблице 1.5. Таблица 1.5
Для второй траектории, Для обеспечения движения рабочей нагрузки по второй траектории наиболее подходящими приводами являются двигатели [1], приведенные в таблице 1.6. Таблица 1.6
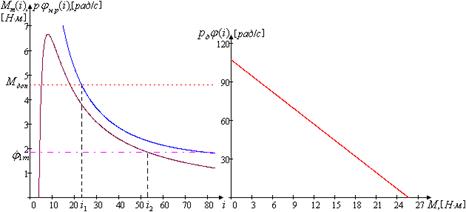
1.4 Выбор передаточного числа редуктораДля определения передаточного числа редуктора привода используется графический метод, позволяющий просто учесть нежесткость механической характеристики двигателя.
По уравнению требуемого момента на валу
двигателя (1.23) строится график зависимости максимального значения момента
где Минимальное значение требуемого Если Выбранный диапазон возможных значений i
корректируют, исходя из условия обеспечения требуемого максимального значения
угловой скорости нагрузки
где На другом графике строят механическую характеристику двигателя по уравнениям:
где
Индексом ном обозначены номинальные параметры выбранного двигателя.
Теперь найдем передаточное число редуктора для каждого выбранного двигателя. 1.4.1 Первый двигатель для первой траекторииЗависимость
Подставим данные двигателя сети ДВИ (таблица
1.5) в уравнение момента (1.27), получим зависимость максимального значения
момента
Найдем значение номинального момента
Используя (1.24) найдем
При помощи программного пакета MathCad построим графики зависимости
максимального момента
Выберем
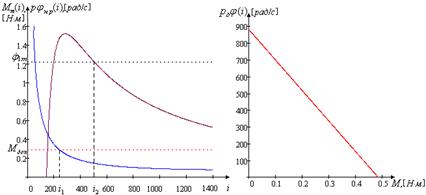
Построим графики зависимости максимального момента и располагаемой скорости нагрузки от передаточного числа редуктора, и механическую характеристику двигателя.
Рис. 1.4. Зависимость максимального момента Рис. 1.5. Механическая и располагаемой скорости нагрузки характеристика двигателя от передаточного числа редуктора Найдем граничные значения
При выборе конкретного значения передаточного числа i редуктора необходимо остановиться на минимально возможном значении из диапазона. Для первого двигателя первой траектории
выбираем 1.4.2 Второй двигатель для первой траекторииПодставим данные двигателя серия СД (таблица
1.5) в уравнение момента (1.27), получим зависимость максимального значения
момента
Найдем значение номинального момента
Используя (1.24) найдем
При помощи программного пакета MathCad построим графики зависимости
максимального момента
Выберем
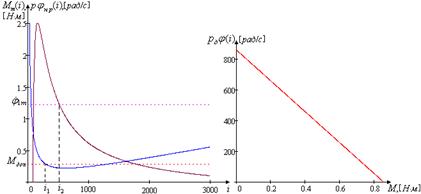
Построим графики зависимости максимального момента и располагаемой скорости нагрузки от передаточного числа редуктора, и механическую характеристику двигателя.
Рис. 1.6. Зависимость максимального момента Рис. 1.7. Механическая и располагаемой скорости нагрузки характеристика двигателя от передаточного числа редуктора Найдем граничные значения
Для второго двигателя первой траектории
выбираем Проведя проверку на нагрев двигателей первой
траектории, мы получили очень высокие значения передаточных чисел ( 1.4.3 Первый двигатель второй траектории По формуле 1.23 найдем зависимость
Подставим данные двигателя серии 2П (таблица 1.6)
в уравнение момента (1.27), получим зависимость максимального значения момента
Используя (1.24) найдем
При помощи программного пакета MathCad построим графики зависимости
максимального момента
Выберем
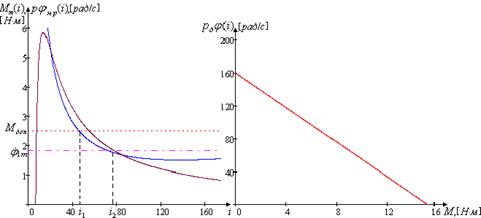
Построим графики зависимости максимального момента и располагаемой скорости нагрузки от передаточного числа редуктора, и механическую характеристику двигателя.
Рис. 1.8. Зависимость максимального момента Рис. 1.9. Механическая и располагаемой скорости нагрузки характеристика двигателя от передаточного числа редуктора Найдем граничные значения
Для первого двигателя второй траектории выбираем
Наиболее подходящим по своим параметрам из найденных в справочных источниках информации редукторов является червячный одноступенчатый редуктор 5Ч 80 [2]. Основные характеристики выбранного редуктора: – максимальный передаваемый крутящий момент – коэффициент полезного действия – подводимая расчетная мощность – масса – передаточное отношение – габариты Максимальный передаваемый крутящий момент на тихоходном (выходном) валу редуктора к валу двигателя
Так, как значение момента 1.4.4 Второй двигатель второй траекторииПодставим данные двигателя серии ДВИ (таблица
1.6) в уравнение момента (1.27), получим зависимость максимального значения
момента
Найдем значение номинального момента
Используя (1.24) найдем
При помощи программного пакета MathCad построим графики зависимости
максимального момента
Выберем
Построим графики зависимости максимального момента и располагаемой скорости нагрузки от передаточного числа редуктора, и механическую характеристику двигателя.
Рис. 1.10. Зависимость максимального момента Рис. 1.11. Механическая и располагаемой скорости нагрузки характеристика двигателя от передаточного числа редуктора Найдем граничные значения
Для второго двигателя второй траектории выбираем
Наиболее подходящим по своим параметрам из найденных редукторов является цилиндрический двухступенчатый редуктор 1Ц2У 100 [4]. Характеристики выбранного редуктора: – максимальный передаваемый крутящий момент – коэффициент полезного действия – масса – передаточное отношение – габариты Максимальный передаваемый крутящий момент на тихоходном (выходном) валу редуктора к валу двигателя определим по формуле 1.29:
Поскольку значение момента 1.5 Проверка двигателя привода на нагревДвигатель будет работать не перегреваясь, если
среднее значение потерь его мощности в якорной цепи
Среднее значение потерь мощности за время
рабочего цикла
Из неравенства (1.30) и уравнения (1.31) следует, что условием нормального теплового режима двигателя является требование:
где
Таким образом, при проверке двигателя на нагрев
необходимо знать закон изменения момента двигателя,
где Режим разгон двигателя. При проверке двигателя на нагрев необходимо учесть, что скорость двигателя не может изменяться мгновенно, поэтому траекторию необходимо сгладить в участках разгона и торможения. Максимально возможный момент двигателя определяется допустимой величиной тока в якорной цепи. Обычно
тогда и момент
Моменту, развиваемому при разгоне, препятствует сила трения, поэтому ускорение в механизме:
Время, необходимое для разгона:
Режим торможение двигателя Режиму торможения способствуют силы трения в
механизмах поворота и силы тяжести нагрузки в механизмах подъема при подъеме
груза. Двигатель должен развивать тот же максимально возможный момент
Время, необходимое для торможения
1.5.1 Проверка на нагрев первого двигателя первой траекторииИз рисунка 1.1 видно, что скорость в моменты времени t=2t1 и t=13t1 изменяется скачком. Двигатель не сможет обеспечить такой режим работы, поэтому необходимо предусмотреть участок разгона и участок торможения. Разобьём время рабочего цикла на 7 интервалов времени: 1. [0; t1], 2. [t1; 2t1-tторм ], 3. [2t1-tторм; 2t1], 4. [2t1; 13t1], 5. [13t1; 13t1+tразг ], 6. [13t1+tразг; 14t1], 7. [14t1; Tц]. Режим разгона Момент, развиваемый двигателем на участке разгона:
Для
первого двигателя первой траектории По формуле 1.38 определим ускорение при разгоне:
Время, необходимое для разгона:
Режим торможения На
участке торможения двигатель должен развивать тот же максимально возможный
момент По формуле 1.40 рассчитаем ускорение при торможении:
Время, необходимое для торможения:
Графики траектории, скорости и ускорения нагрузки, с учётом введённых участков разгона и торможения, показаны на рис. 1.12.
Рис. 1.12. Первая измененная траектория рабочего цикла Состояние покоя Момент, требуемый от двигателя на любом из участков траектории, определяется в соответствие с (1.14) и (1.23):
Рассчитывая моменты для любого из участков
траектории, рассуждаем следующим образом: составляющие уравнения 1.42, в
которые входит ускорение, берем с теми знаками, как показывает диаграмма. Знак
статического момента, приведенного к валу двигателя, выбираем так: если
сопротивление нагрузки помогает режиму на данном участке (например, режим
торможения), тогда знак статического момента берется противоположным знакам
слагаемых, в которые входит Таблица 1.7
При расчете момента Из таблицы видно, что Находим эквивалентный момент двигателя по формуле (1.33):
Проверяем условие нормального теплового режима:
Поскольку условие выполняется, значит,
двигатель типа ДВИ-211–02 с передаточным числом Определим энергетический запас двигателя, используемого при отработке первой траектории:
1.5.2 Проверка на нагрев второго двигателя первой траекторииИз пункта 1.4.2 возьмем значение номинального момента:
Режим разгона Момент, развиваемый двигателем на участке разгона:
Для второго
двигателя первой траектории По формуле 1.38 определим ускорение при разгоне:
Время, необходимое для разгона:
Режим торможения На
участке торможения двигатель должен развивать тот же максимально возможный
момент По формуле 1.40 рассчитаем ускорение при торможении:
Время, необходимое для торможения:
Момент, требуемый от двигателя на любом из участков траектории, определяется по формуле 1.42. Таблица 1.8
Из таблицы видно, что Находим эквивалентный момент двигателя по формуле (1.33):
Проверяем условие нормального теплового режима:
Поскольку условие выполняется, значит,
двигатель типа СД-150 с передаточным числом Определим энергетический запас двигателя: 1.5.3 Проверка на нагрев первого двигателя второй траекторииИз пункта 1.4.3 возьмем значение номинального момента:
Для
второго двигателя первой траектории выбираем Момент, требуемый от двигателя на любом из участков траектории, определяется по формуле 1.42. Таблица 1.8
Находим эквивалентный момент двигателя по формуле (1.33):
Проверяем условие нормального теплового режима:
Поскольку условие выполняется, значит,
двигатель типа 2ПБ90МУХЛ4 с передаточным числом Определим энергетический запас двигателя:
1.5.4 Проверка на нагрев второго двигателя второй траекторииИз пункта 1.4.4 возьмем значение номинального момента:
Для
второго двигателя первой траектории выбираем Момент, требуемый от двигателя на любом из участков траектории, определяется по формуле 1.42. Таблица 1.9
Находим эквивалентный момент двигателя по формуле (1.33):
Проверяем условие нормального теплового режима:
Поскольку условие выполняется, значит,
двигатель типа ДВИ-321–02 с передаточным числом Определим энергетический запас двигателя:
1.6 Выбор рабочей траекторииДля выбора программной траектории движения нагрузки необходимо проанализировать достоинства и недостатки каждой из двух возможных траекторий, а также пар двигателей, чтобы в итоге остановиться на одной траектории и выбрать один из четырех двигателей. Сравним двигатели, выбранные для данных
траекторий. Скорости вращения двигателей типа ДВИ-211–02 и СД-150 для первой
траектории очень большие ( Как для первой, так и для второй траектории, все двигатели обеспечивают достаточный энергетический запас, но двигатели для второй траектории типа 2ПБ90МУХЛ4 и ДВИ-321–02 обеспечивают больший запас энергии. Необходимо отметить, что изменения, которым подвергается первая программная траектория, снижают качество управляемого привода. Остановим свой выбор на второй из двух возможной траекторий. Для второй траектории движения необходимо выбрать двигатель из двух возможных 2ПБ90МУХЛ4 и ДВИ-321–02. Сравнивая технические характеристики двигателей (таблица 1.6), можем отметить, что двигатель 2ПБ90МУХЛ4 обладает меньшей массой по сравнению с двигателем ДВИ-321–02, и меньшим сопротивлением в якорной цепи, что уменьшает тепловые потери, и меньшим энергетическим запасом. Таким образом, выбираем двигатель типа
2ПБ90МУХЛ4 и соответственно подобранный для него редуктор 5Ч 80 типа
червячный одноступенчатый с передаточным отношением 2. Синтез системы управления электроприводом2.1 Выбор информационных элементов приводаИнформационными элементами привода являются элементы измерителя рассогласований: задающее устройство, датчик обратной связи, сумматор. Вид управляемого привода обуславливает выбор типа информационных элементов: датчиков линейных или угловых перемещений. Приведем статическую ошибку системы, заданную в ТЗ в относительных единицах, к абсолютным единицам.
Допустимая погрешность измерителя
рассогласования
Ошибка измерителя рассогласования
Будем считать, что датчики ДОС и ЗУ абсолютно идентичны, поэтому они вносят одинаковый вклад в статическую ошибку измерителя рассогласования.
Тогда из выражения 2.4 статические ошибки ДОС и ЗУ:
При выборе информационных элементов необходимо исходить из требований технического задания на разработку привода: ·
вида управляемого привода и статической
погрешности датчика ·
максимальных перемещений ·
скорости Исходя из выше изложенных требований к информационным элементам, выберем потенциометр проволочный, характеристики которого представлены в таблице 2.1. Таблица 2.1. Параметры выбранного датчика
2.2 Синтез структурной схемы управляемого приводаСинтез структурной схемы привода начинают с разработки его функциональной схемы.
Рис. 2.1. Функциональная схема управляемого привода На рис. 2.1 обозначено: ЗД − задающий датчик (преобразовывает механический сигнал в электрический); ЭС − элемент сравнения (в данном случае сумматор); КУ − корректирующее устройство; УМ − усилитель мощности (формирует напряжение в якорную цепь двигателя); Дв – двигатель, преобразующий напряжение на его входе в угловое перемещение на его выходном валу; Ред – редуктор, понижающий значение углового перемещения на выходном валу двигателя до величины перемещения, необходимого для управления положением рабочей нагрузки; ДОС – датчик обратной связи, обеспечивающий преобразование физического сигнала в форму, удобную для сравнения. Линеаризованная структурная схема двигателя постоянного тока (ДПТ) с независимым возбуждением при управлении по цепи якоря, составленная для приращений переменных двигателя в относительных единицах (о.е.), представлена на рис. 2.2.
Рис. 2.2. Линеаризованная структурная схема ДПТ в о.е. На схеме (рис. 2.2) обозначено:
где
За
базовые значения угловой скорости вала двигателя Двигатель имеет переменный параметр – Для использования структурной схемы двигателя в общей структуре привода необходимо осуществить в схеме переход от относительных единиц измерения (о.е.) к абсолютным единицам (а.е.). Передаточные функции двигателя по управляющему и возмущающему воздействиям в а.е. могут быть получены из соответствующих им выражений в о.е. при использовании базовых значений параметров, выбранных для совершения прямого перехода в схеме. За базовое значение магнитного потока двигателя
Используя структурную схему двигателя в
относительных единицах (рис. 2.2) и приведенные выше базовые значения
переменных, преобразуем схему, введя масштабирующие коэффициенты,
обеспечивающие измерение в абсолютных единицах передаточных функций двигателя
по управляющему
Рис. 2.3. Линеаризованная структурная схема ДПТ с передаточными функциями в абсолютных единицах (а.е.) Приведем все необходимые параметры для дальнейших расчетов схемы. Двигатель 2ПБ90МУХЛ4
Редуктор червячный одноступенчатый 5Ч 80
Траектория рабочего цикла
Магнитный поток двигателя в рабочей точке (формула 2.6):
Относительное сопротивление якорной цепи (формула 2.7):
Возмущающее воздействие
Для нахождения механической постоянной
двигателя
Минимальное и максимальное значение механической постоянной двигателя
Передаточная функция двигателя по управляющему воздействию
Разделим числитель и знаменатель передаточной
функции на
Найдем минимальное и максимальное значение
электромеханической постоянной времени двигателя
Заметим, что если представить, что
Если Если Определим параметры данной передаточной функции из следующей пары уравнений:
Из уравнения 2.12 выразим параметр
Из уравнения (2.11) определим минимальное и
максимальное значения постоянной времени
Определим значения параметра
Найденные значения
Решим уравнение (2.14):
Корни уравнения:
где
Аналогично решим уравнение 2.15:
Корнями данного уравнения являются:
Таким образом, получим:
Определим коэффициент передачи двигателя:
Передаточная функция двигателя по возмущающему воздействию
Разделим числитель и знаменатель передаточной
функции на
Заметим, что знаменатель передаточной функции двигателя по возмущающему воздействию совпадает со знаменателем передаточной функции по управляющему воздействию. Поэтому представим знаменатель функции (2.18) в следующем виде:
Коэффициенты передачи двигателя:
Для дальнейшего использования составим таблицу со всеми найденными параметрами передаточных функций двигателя (таблицу 2.2). Таблица 2.2. Значения параметров ПФ двигателя
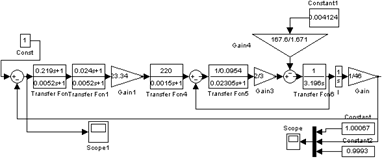
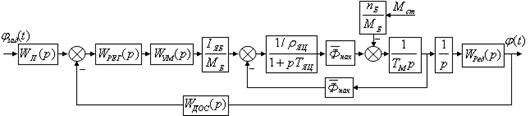
Изобразим структурную схему управляемого привода (рис. 2.4).
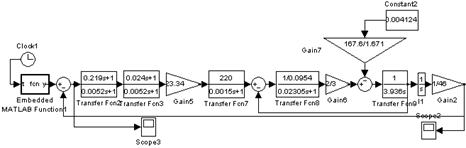
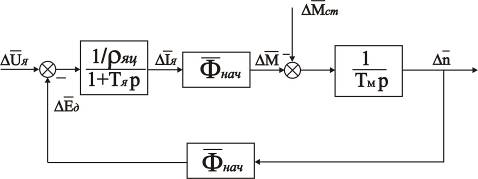
Рис. 2.4. Структурная схема управляемого привода Передаточные функции отдельных звеньев привода: – – – – – – – 2.3 Синтез структуры регулятораВ структуре управляемого привода два модуля: силовой и управляющий. Управляющий модуль состоит из измерителя рассогласований и регулятора. Для того чтобы система удовлетворяла требованиям технического задания, необходимо провести синтез регулятора. При помощи правил преобразования структурной
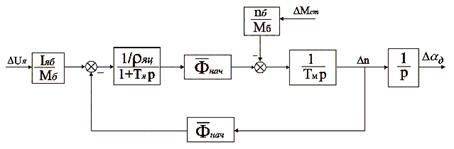
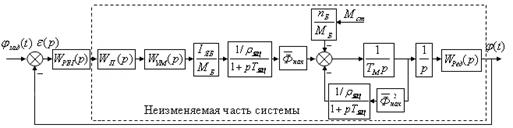
схемы, перенесем звено
Рис. 2.5. Преобразованная структурная схема привода Запишем передаточную функцию неизменяемой части системы:
где Выражение 2.19 при минимальной и максимальной нагрузках примет следующий вид:
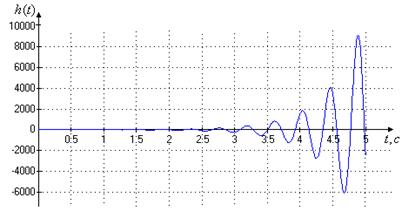
Проанализируем устойчивость исходной системы и соответствие системы требованиям по качеству. Об устойчивости системы можно судить по ее реакции на единично ступенчатую функцию, т.е. по ее переходной характеристике. Построим соответствующие графики в программном пакете MATLAB. Графики переходной характеристики представлены на рис. 2.6 – 2.7.
Рис. 2.6. Переходная характеристика исходной системы при минимальной нагрузке на управляемый привод
Рис. 2.7. Переходная характеристика исходной системы при максимальной нагрузке на управляемый привод Таким образом, мы получили, что исходная система не устойчива. Необходимо введение в исходную систему корректирующего устройства (КУ) для обеспечения требуемого качества как в установившемся (задано в виде динамической ошибки), так и в переходном (ограничения на прямые показатели качества) режимах. Проведем синтез при помощи метода логарифмических амплитудно-частотных характеристик (ЛАЧХ). Разобьем синтез на условные стадии: 1) Построение ЛАЧХ исходной системы. 2) Построение желаемой ЛАЧХ в соответствие с требованиями ТЗ. 3) Определение передаточной функции КУ. 1) Для построения логарифмических амплитудно-частотных характеристик (ЛАЧХ) неизменяемой части системы проведем расчеты.
Осуществим переход:
2)
В ТЗ заданы относительная динамическая
ошибка, максимальные скорость и ускорение траектории движения. В соответствие с
этим для построения границы запретной области необходимо найти координаты
контрольной точки
В соответствие с (2.22–2.23) найдем
Таким образом, Для
того чтобы входное воздействие воспроизводилось с ошибкой, не превосходящей
динамическую ошибку, ЛАЧХ системы не должна попадать в запретную область. По рис. 2.8 можно сделать вывод о
выполнении требования ТЗ по качеству системы в установившемся режиме, т.к. при
минимальном и максимальном значениях электромеханической постоянной двигателя Среднечастотный участок определяет устойчивость и запасы устойчивости системы, а, следовательно, и качество системы в переходном режиме. Для построения среднечастотного участка будем использовать методику Бесекерского [3, с. 369]. Для определения левой и правой границ среднечастотного участка используются неравенства:
где
Значение Подставим значения в формулу 2.24:
В формулу подставляем значение показателя
колебательности: Таким образом,
где Сначала рассчитаем значение
Для вычисления Исходные данные:
По правилу сначала нужно вычесть наименьшие
постоянные времени, поэтому отнимем от
Найдем значение
Таким образом, мы рассчитали значения границ среднечастотного участка:
Расширяя среднечастотный участок, мы добьемся требуемого качества
в переходном режиме. Левую границу будем смещать до тех пор, пока не будет
выполняться требуемое значение запаса по модулю Высокочастотный участок определяет
помехозащищенность системы, поэтому наклон высокочастотных асимптот должен быть
большим. В то же время с целью упрощения модели корректирующего устройства
высокочастотные асимптоты 3) Определим передаточную функцию регулятора. Построение
Определим передаточную функцию последовательного КУ:
Составим передаточную функцию
По формуле 2.26 найдем
2.4 Обеспечение требуемой точности проектируемого приводаВ ТЗ на проектирование указаны допустимые
статическая Статическая ошибка системы оценивается в
типовом режиме: при постоянных значениях задающего и возмущающего воздействий.
В п. 2.1 уже использовалась допустимая
где
Таким образом, статическая погрешность элементов прямого канала Статическая погрешность по задающему значению Статическая погрешность привода по возмущающему воздействию Определим допустимую статическую погрешность привода по возмущающему воздействию:
Для определения ошибки скорректированной системы по возмущающему воздействию воспользуемся методом коэффициентов ошибок, описываемым формулой [3, с. 198]:
где
Найдем передаточную функцию
Таким образом, получили, что Далее проведем оценку динамической точности системы. Допустимая динамическая ошибка системы Амплитуда ошибки определяется по формуле:
где Найдем значение динамической ошибки при минимальной и максимальной нагрузках на управляемый привод:
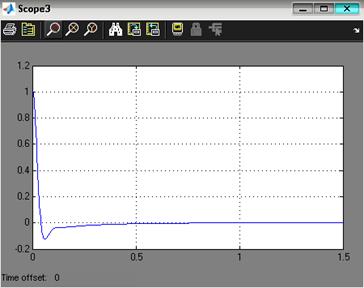
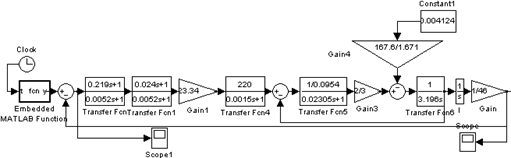
Таким образом, рассчитанная динамическая ошибка системы 3. Моделирование спроектированного управляемого привода3.1 Модель скорректированной системы при отработке ступенчатого сигнала3.1.1 Цифровая модель скорректированной системы при отработке ступенчатого сигнала при минимальной нагрузке на управляемый приводНа рис. 3.1 приведена цифровая модель скорректированной системы при отработке ступенчатого сигнала при минимальной нагрузке на управляемый привод, разработанная в программном пакете MATLAB версии 7.3.
Рис. 3.1. Цифровая модель скорректированной системы при отработке ступенчатого сигнала при минимальной нагрузке на управляемый привод
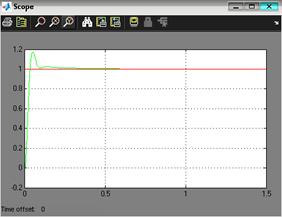
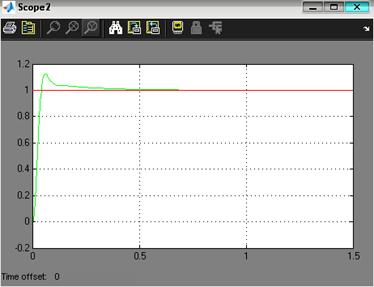
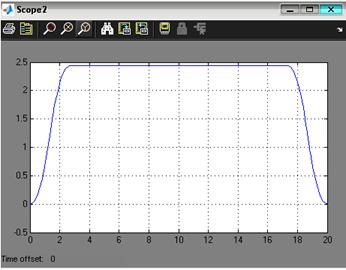
Рис. 3.2. Реакция выхода системы на единичный ступенчатый сигнал при минимальной нагрузке По графику (рис. 3.2) найдем установившееся и
максимальное значения
Расчетное выражение для перерегулирования:
Для определения время регулирования
Определим прямые показатели качества желаемой системы при минимальной массе нагрузки на проектируемый привод и сравним с соответствующими значениями, заданными в ТЗ: Требования ТЗ:
Реальные значения показателей определим по формулам 3.1 – 3.2:
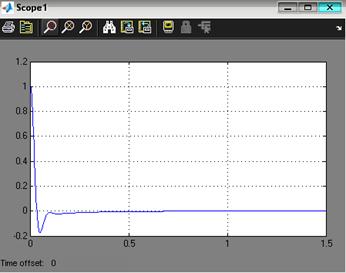
Границы коридора: Статическую ошибку системы можно определить по графику ошибки, представленном на рис. 3.3.
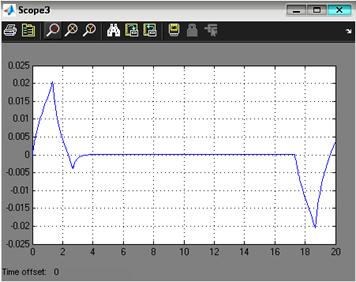
Рис. 3.3. Ошибка системы при отработке ступенчатого сигнала при минимальной массе нагрузки на управляемый привод В ТЗ определена статическая допустимая погрешность:
Реальное значение ошибки: 3.1.2 Цифровая модель скорректированной системы при отработке ступенчатого сигнала при максимальной нагрузке на управляемый приводЦифровая модель скорректированной системы при отработке ступенчатого сигнала при максимальной массе нагрузки на управляемый привод представлена на рис. 3.4.
Рис. 3.4. Цифровая модель скорректированной системы при отработке ступенчатого сигнала при максимальной нагрузке на управляемый привод
Рис. 3.5. Реакция выхода системы на единичный ступенчатый сигнал при максимальной нагрузке По графику (рис. 3.5) найдем установившееся и
максимальное значения
Реальные значения показателей:
Рис. 3.6. Ошибка системы при отработке ступенчатого сигнала при максимальной массе нагрузки на управляемый привод Результаты моделирования приведены в приложении 5. Реальное значение ошибки: Требование ТЗ к статической точности: Проанализировав найденные показатели качества скорректированной системы, можно сделать, что полученная скорректированная система удовлетворяет заданным требованиям к качеству переходного процесса и статической точности, как при минимальной, так и при максимальной массе нагрузки на управляемый привод. 3.2 Модель желаемой системы при отработке выбранной траектории3.2.1 Цифровая модель скорректированной системы при отработке выбранной траектории движения при минимальной нагрузке на управляемый приводНа рис. 3.7 представлена цифровая модель скорректированной системы при отработке выбранной траектории движения при минимальной массе нагрузки, построенная в программной среде MATLAB.
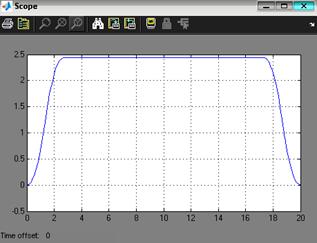
Рис. 3.7. Цифровая модель скорректированной системы при отработке программной траектории при минимальной нагрузке на управляемый привод
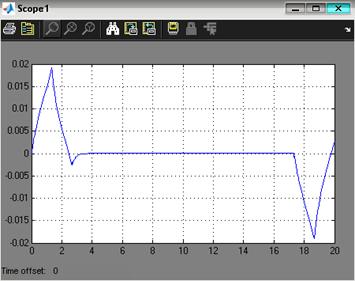
Рис. 3.8. Реакция выхода системы при отработке программной траектории движения при минимальной массе нагрузки на управляемый привод Динамическую ошибку системы определим по графику ошибки, представленном на рисунке 3.9.
Рис. 3.9. Ошибка системы при отработке программной траектории движения при минимальной массе нагрузки на управляемый привод
Реальное значение ошибки: Требование ТЗ к динамической точности: 3.2.2 Цифровая модель скорректированной системы при отработке программной траектории движения при максимальной массе нагрузки на управляемый приводНа рис. 3.10 представлена цифровая модель скорректированной системы при отработке выбранной траектории движения при максимальной массе нагрузки, построенная в программном пакете MATLAB.
Рис. 3.10. Цифровая модель скорректированной системы при отработке программной траектории при максимальной нагрузке на управляемый привод
Рис. 3.11. Реакция выхода системы при отработке программной траектории движения при минимальной массе нагрузки на управляемый привод Динамическую ошибку системы определим по графику ошибки, представленном на рисунке 3.12.
Рис. 3.12. Ошибка системы при отработке программной траектории движения при минимальной массе нагрузки на управляемый привод
Реальное значение ошибки: Требование ТЗ к динамической точности: Цифровая модель спроектированного электропривода для максимальной и минимальной массы нагрузки удовлетворяет ограничению на динамическую ошибку, представленному в ТЗ. ЗаключениеВ курсовом проекте был разработан электропривод, предназначенный для программного управления линейным перемещением механизма подъёма промышленного робота-манипулятора. При выполнении первого этапа проекта рассматривались две программные траектории перемещения нагрузки, предложенные в техническом задании, для которых были рассчитаны параметры (скорость, ускорение). Для каждой из траекторий были определены нагрузки, действующие на привод, выбран двигатель и редуктор, проведена проверка двигателя и редуктора на нагрев. Далее ввиду функциональных особенностей привода была выбрана оптимальная траектория. На втором этапе проектирования выбраны информационные элементы (потенциометры) по заданной статической точности, проведен синтез регулятора. На следующем этапе был проведено моделирование цифровой модели спроектированного электропривода с помощью программного пакета MATLAB. Полученная цифровая модель отвечала всем требованиям технического задания по точности и качеству. Соответствие характеристик рассчитанной системы требованиям технического задания приведено в таблице 4. Таблица 4. Сравнение результатов, полученных при выполнении проекта
Спроектированный электропривод удовлетворяет всем требованиям ТЗ как при минимальной, так и при максимальной массах нагрузки. Список литературы 1. Подлинева Т.К., Устюгов М.Н. Проектирование управляемого привода в электромеханических системах: Учебное пособие по курсовому проектированию. 2. http://www.izh-reduktor.ruproductionscherv_reductsreduktoryi _odnostupenchatyie _tipa_5ch.html. 3. Бесекерский В.А., Попов Е.П. Теория систем автоматического управления. – СПб: Профессия, 2003 – 752с. 4. http://www.1000a.ru/catalog-12.htm. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
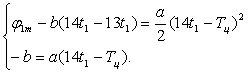 . (1.3)
. (1.3)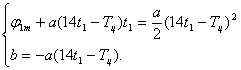 . (1.4)
. (1.4)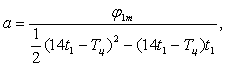 (1.5)
(1.5)
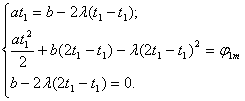 , (1.7)
, (1.7)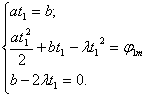 . (1.8)
. (1.8)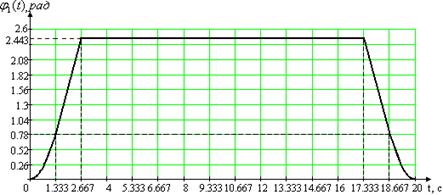
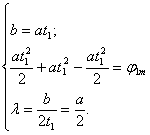 , (1.10)
, (1.10)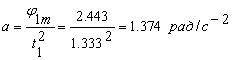 ,
, 
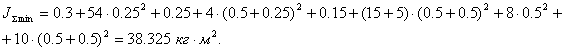
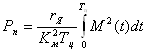 . (1.31)
. (1.31)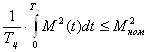 , (1.32)
, (1.32)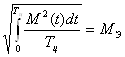 ,
,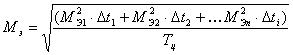 , (1.34)
, (1.34) . (1.35)
. (1.35)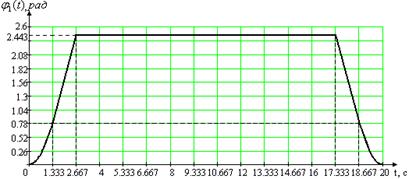
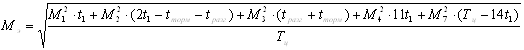
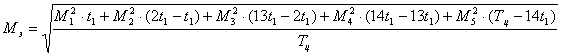
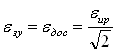 . (2.5)
. (2.5)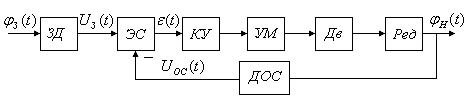
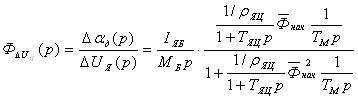 ,
,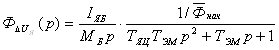 , где
, где 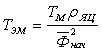 .
.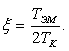 (2.13)
(2.13)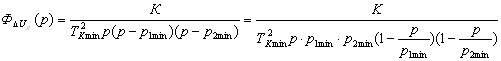 ,
,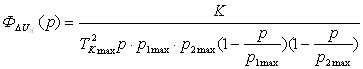 .
.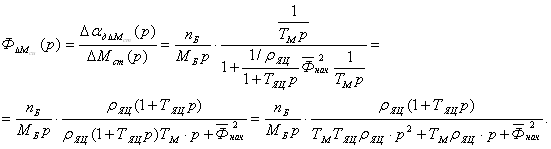
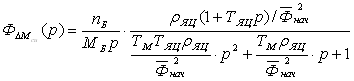 .
.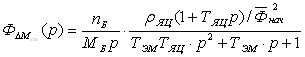 . (2.18)
. (2.18)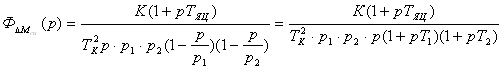 , где
, где 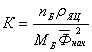 .
.
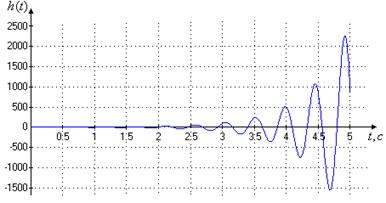
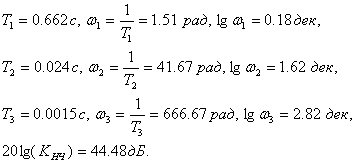
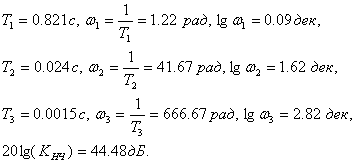
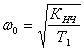 –
базовая частота,
–
базовая частота,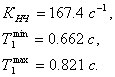
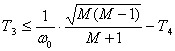 , (2.25)
, (2.25)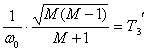 .
.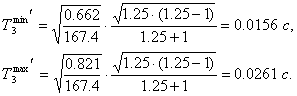
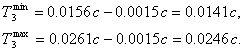
 .
.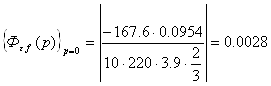 .
.