Курсовая работа: Расчет режима обжатий на обжимном реверсивном станеКурсовая работа: Расчет режима обжатий на обжимном реверсивном стане1. Расчет режима обжатий 1.1 Расчет максимального обжатия 1.1.1 Максимальное обжатие по условию захвата металла валками В
соответствии с рекомендациями принимаем Тогда рабочий диаметр валков определим по формуле [2, стр. 27]:
в первом калибре:
в остальных калибрах:
Определяем
окружную скорость валков при
в первом калибре:
в остальных калибрах:
По таблице
2.1 [1, стр. 23] допустимый угол захвата при прокатке на гладкой бочке валков – 22,460 в калиброванных валках без насечки – 24,560 в калиброванных валках с насечкой – 30,020 Определяем максимальное обжатие [2, стр. 6]:
в первом калибре:
для калиброванных валков без насечки:
для калиброванных валков с насечкой:
1.1.2 Максимальное обжатие по мощности электродвигателя По таблице 2 [2, стр. 14] для двух электродвигателей П34–160–9К находим: номинальный
крутящий момент маховой
момент якоря электродвигателей частота
вращения электродвигателей допустимый
момент перегрузки Допустимый момент электродвигателей определим по формуле [2, стр. 11]:
Далее определяем: приведенный маховой момент [2, с. 13]:
динамический
момент при
момент холостого хода [2, стр. 13]:
Находим
допустимый крутящий момент прокатки на валках блюминга при
Размеры
поперечного сечения слитка посередине
Относительное обжатие рассчитаем по формуле [2, стр. 9]:
Определим рабочий радиус [2, стр. 9]:
Скорость
деформации при
Сопротивление деформации зависит от марки металла, его температуры, степени и скорости деформации, для стали 60с2 рассчитывается по формуле Б.П. Бахтинова [1, с. 25]:
По данным [3]
для стали 60с2 находим:
Находим длину очага деформации [2, стр. 7]:
Фактор формы очага деформации [1, стр. 24]:
Коэффициент
напряженного состояний, учитывающий влияние на контактное давление внешнего
трения n зависит от фактора формы очага деформации Коэффициент nж рассчитывают по эмпирической формуле [2, стр. 9]:
nж – коэффициент, учитывающий влияние внешних зон по отношению к геометрическому очагу деформации.
Коэффициент n учитывает влияние ширины раската. При прокатке на блюминге принимается равным 1,15. Контактное давление по формуле А.И. Целикова [2, стр. 7]:
Определим
Находим длину
очага деформации, принимая
Bср – средняя ширина слитка, мм.
Определим максимальное обжатие по мощности электродвигателей [2, стр. 15]:
Повторяем расчет
при
Принимаем 1.1.3 Максимальное обжатие по прочности валков В
соответствии с рекомендациями [2, стр. 17] для блюминга 1100 принимаем
длину бочки валков
Тогда получим [2, стр. 30]:
Для
используемых стальных кованых валков принимаем допустимое напряжение на изгиб Находим допустимое усилие прокатки [2, с. 16]:
L – длина бочки валков, мм.
Определяем
максимальное обжатие по прочности валков при
1.1.4 Выбор максимального обжатия В результате
расчетов получили значения по условию
захвата валками по мощности
электродвигателей по прочности
валков Окончательно
принимаем 1.2 Среднее обжатие за проход и число проходов Определим
среднее обжатие за проход Числовой коэффициент принимаем равным 0,9 – так как, слиток и блюм имеют разные сечения [2, стр. 17].
Находим число
проходов, необходимое для прокатки блюмов сечением
Так как, по
предварительным расчетам число проходов Уточняем среднее обжатие [2, стр. 19]:
1.3 Предварительная схема обжатий Составляем предварительную схему обжатий. Принимаем первую кантовку после второго прохода. Таблица 1. Предварительная схема обжатий при прокатке блюмов сечением 250×250 на блюминге 1100
1.4 Окончательная схема обжатий Составляем окончательную схему обжатий с учетом уширения по кривым А.Ф. Головина [2, стр. 21]. Результаты уширения приведены в таблице 2. Окончательная
схема обжатий при прокатке блюмов сечением 250×250 мм из слитка Таблица 2. Результаты уширения по методу А.Ф. Головина при прокатке блюмов сечением 250х250 мм на блюминге 1100
Таблица 3. Окончательная схема обжатий при прокатке блюмов сечением 250×250 мм на обжимном реверсивном стане 1100
1.5 Длина раската и коэффициент вытяжки по проходам В первом и втором проходах длину раската принимаем равной длине слитка, а именно 1500 мм. Рассчитаем длину раската и коэффициент вытяжки в третьем проходе. Площадь поперечного сечения раската составит:
Объем обжатого металла найдем следующим образом:
Длина раската составит [2, с. 22]:
Коэффициент вытяжки определим по формуле [2, стр. 22]:
Рассчитаем длину раската и коэффициент вытяжки в четвертом проходе. Площадь поперечного сечения раската составит:
Объем обжатого металла найдем следующим образом:
Длина раската составит:
Коэффициент вытяжки определим по формуле:
Рассчитаем длину раската и коэффициент вытяжки в пятом проходе. Площадь поперечного сечения раската составит:
Объем обжатого металла найдем следующим образом:
Длина раската составит:
Коэффициент вытяжки определим по формуле:
Рассчитаем длину раската и коэффициент вытяжки в шестом проходе. Площадь поперечного сечения раската составит:
Объем обжатого металла найдем следующим образом:
Длина раската составит:
Коэффициент вытяжки определим по формуле:
Рассчитаем длину раската и коэффициент вытяжки в седьмом проходе. Площадь поперечного сечения раската составит:
Объем обжатого металла найдем следующим образом:
Длина раската составит:
Коэффициент вытяжки определим по формуле:
Рассчитаем длину раската и коэффициент вытяжки в восьмом проходе. Площадь поперечного сечения раската составит:
Объем обжатого металла найдем следующим образом:
Длина раската составит:
Коэффициент вытяжки определим по формуле:
Рассчитаем длину раската и коэффициент вытяжки в девятом проходе. Площадь поперечного сечения раската составит:
Объем обжатого металла найдем следующим образом:
Длина раската составит:
Коэффициент вытяжки определим по формуле:
Рассчитаем длину раската и коэффициент вытяжки в десятом проходе. Площадь поперечного сечения раската составит:
Объем обжатого металла найдем следующим образом:
Длина раската составит:
Коэффициент вытяжки определим по формуле:
Рассчитаем длину раската и коэффициент вытяжки в одиннадцатом проходе. Площадь поперечного сечения раската составит:
Объем обжатого металла найдем следующим образом:
Длина раската составит:
Коэффициент вытяжки определим по формуле:
Результаты
расчетов длины раската L1, коэффициентов вытяжки Таблица 4. Длина
раската L1, коэффициенты вытяжки
2. Определение размеров калибров Определяем размеры калибров и составляем эскизы валков. Рекомендуемая глубина ручья при отношении сторон раската Н/В£1,3 [1, стр. 33]
во втором
калибре в третьем
калибре в четвертом
калибре в пятом
калибре С целью
сокращения числа ступеней станинных роликов примем у второго, третьего и
четвертого калибров глубину ручьев одинаковой Глубина ручья
у первого калибра принята, как указывалось выше, 60 мм, следовательно, Определим размеры второго калибра Ширина калибра по дну ручья находится по формуле [1, стр. 34]:
Ширина калибра по буртам [1, с. 34]:
Выпуск калибра определим следующим образом [1, стр. 44]:
Радиусы закругления в калибрах принимаются в соответствии с рекомендованными значениями [1, стр. 34]:
Из указанного
интервала принимаем Определим размеры третьего калибра Ширина калибра по дну ручья:
Ширина калибра по буртам:
Выпуск калибра:
Радиусы закругления в калибрах:
Из указанного
интервала принимаем Определим размеры четвертого калибра Ширина калибра по дну ручья:
Ширина калибра по буртам:
Выпуск калибра:
Радиусы закругления в калибрах:
Для
последнего калибра принимаем Определим размеры пятого (последнего) калибра Ширина калибра по дну ручья:
Ширина калибра по буртам в последнем калибре определяется по формуле [2, с. 36]:
Выпуск калибра: В последнем
калибре Радиусы закругления в последнем калибре [1, стр. 34]:
H – сторона квадрата
Для
последнего калибра принимаем Определим размеры первого калибра Ширина по буртам определена по разности между длинной бочки валков и шириной буртов [2, стр. 36]:
Ширина по дну
при выпуске
Радиусы
закругления принимаем Показания циферблата найдем по формуле [1, с. 34]:
·
для
первого прохода ·
для
второго прохода ·
для
третьего прохода ·
для
четвертого прохода ·
для
пятого прохода ·
для
шестого прохода ·
для
седьмого прохода ·
для
восьмого прохода ·
для
девятого прохода ·
для
десятого прохода ·
для
одиннадцатого прохода Показания циферблата указаны в таблице 4. Размеры калибров приведены в таблице 5 Таблица 5. Размеры калибров
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
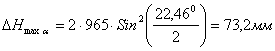
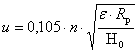 , где (1.12)
, где (1.12)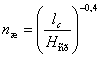 , где (1.16)
, где (1.16)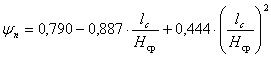 , где (1.18)
, где (1.18)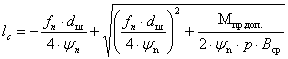 , где (1.19)
, где (1.19)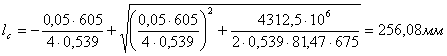
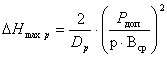 , где (1.24)
, где (1.24)