Курсовая работа: Редуктор двухступенчатый соосный двухпоточныйКурсовая работа: Редуктор двухступенчатый соосный двухпоточныйФЕДЕРАЛНОЕ АГЕНСТВО ПО КУЛЬТУРЕ И КИНЕМАТОГРАФИИ САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ КИНО И ТЕЛЕВИДЕНИЯ Кафедра механики Расчетно-пояснительная записка к курсовому проекту на тему «Редуктор двухступенчатый соосный двухпоточный с внутренним зацеплением тихоходной ступени» Санкт-Петербург 2009г. Содержание
Техническое задание на курсовое проектирование Механизм привода
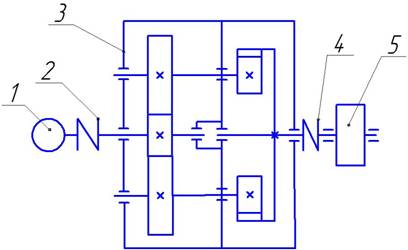
1- электродвигатель; 2- муфта; 3- редуктор зубчатый цилиндрический двухступенчатый соосный двухпоточный с внутренним зацеплением тихоходной ступени; 4- муфта; 5- исполнительный механизм. Вариант 1 Потребный момент на валу исполнительного механизма (ИМ) Тим=30Нм; Угловая скорость вала ИМ ωим=5,8с-1. Разработать: 1- сборочный чертеж редуктора; 2- рабочие чертежи деталей тихоходного вала: зубчатого колеса, вала, крышки подшипника. 1 Кинематический расчет и выбор электродвигателя Исходные данные: - потребный момент на валу исполнительного механизма (ИМ) Тим=30Нм; - угловая скорость вала ИМ ωим=5,8с-1; Определяем мощность на валу ИМ Nим= Тимх ωим=30х5,8=174Вт. Определяем общий КПД привода по схеме привода ηобщ=ηкп ηшп ηм ηп (1.1) где [1, с.9,10]: ηзп=0,972- КПД зубчатой цилиндрической передачи; ηм=0,982 – потери в муфтах; ηп=0,994- коэффициент, учитывающий потери на трение в подшипниках 4-х валов. Сделав подстановку в формулу (1.1) получим: ηобщ.=0,972*0,982*0,994=0,868 Определяем потребную мощность электродвигателя [1,с.9] Nэд≥Nим/ηобщ. (1.2) где Nэд – требуемая мощность двигателя: Nэд=174/0,877=198,4Вт Выбираем электродвигатель [1,с.18,табл.П2] Пробуем двигатель АИР71В8: Nдв.=0,25кВт; nдв=750об/мин; S=8%. Определяем номинальную частоту вращения электродвигателя по формуле (5) [1,c.11]: nном=nдв·(1-S/100); nном=750·(1-0,08); nном=690 об/мин Определяем угловую скорость вала двигателя ωдв=πnдв/30=π*690/30=72,2рад/с; Определяем общее передаточное число привода U=ωдв./ωим=72,2/5,8=12,5 Производим разбивку передаточного числа по ступеням. По схеме привода Uобщ.=U1· U2; (1.3) Назначаем по рекомендации [1,табл.2.3]: U2=5; тогда U1= Uобщ./U2; U1=2,5. Принимаем окончательно электродвигатель марки АИР71В8. Угловые скорости определяем по формуле ω=πn/30 (1.4)
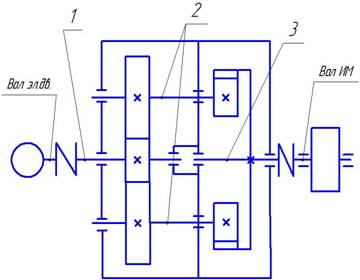
Рис.1 Схема валов привода 1 – быстроходный вал; 2 – промежуточный вал; 3 – тихоходный вал. По схеме валов (рис.1) и формуле (1.4) определяем частоты вращения и угловые скорости каждого вала n1= nном. ω1= ωдв=72,2рад/с; n2= nном/U1=650/3,5=185,7об/мин; ω2=πn2/30=π*216,7/30=19,45 рад/с; n3= n2/U2=216,7/3,55=52,3 об/мин; ω3=πn3/30=π*61,1/30=5,48 рад/с. Определяем мощность на каждом валу по схеме привода N1=Nдв ηм=0,25*0,98=245Вт; N2=N1 ηзп ηп3=245*0,97*0,993=230Вт; N3=N2 ηзп ηп =233*0,97*0,99=221Вт; Nим=N3 ηм =224*0,98=217Вт. Определяем вращающие моменты на каждом валу привода по формулам [1,с.12,14]:
Т1=245/72,2=3,4 Н•м; Т2=3,4•2,5=8,5 Н•м; Т3=8,5•5=42,5 Н•м. Все рассчитанные параметры сводим в табл.1. Таблица 1 Параметры кинематического расчета
2 Выбор материалов и определение допускаемых напряжений Выбираем материал для шестерни и колеса по табл.3.2 [4,c.52]: шестерня – сталь 40Х, термообработка – улучшение 270НВ, колесо - сталь 40Х, термообработка – улучшение 250НВ. Определяем допускаемое контактное напряжение по формуле [4,c.53]:
где σHlimb – предел контактной выносливости при базовом числе циклов; КHL – коэффициент долговечности; [SH] – коэффициент безопасности; по [1,c.33]: КHL =1; [SH] =1,1. Определяем σHlimb по табл.3.1[4,c.51]: σHlimb =2НВ+70; (2.2) σHlimb1 =2×270+70; σHlimb1 =610МПа; σHlimb2 =2×250+70; σHlimb1 =570МПа. Сделав подстановку в формулу (2.1) получим
Определяем допускаемое расчетное напряжение по формуле [4,c.53]:
Определяем допускаемые напряжения по по табл.3.1[4,c.51]: [σ]Fo =1,03НВ; [σ]Fo1 =1,03x270=281МПа; [σ]Fo2 =1,03x250=257МПа. 3 Расчет тихоходной ступени привода 3.1 Проектный расчет Определяем межосевое расстояние передачи по формуле [4,c.61]:
где Ка – числовой коэффициент, Ка =49,5 [4,c.61]; КHβ – коэффициент, учитывающий неравномерность распределения нагрузки по ширине венца, КHβ =1 для прямозубых колес [4,c.54];
U – передаточное отношение, U2=5 (см. табл.1): Т – вращающий момент на колесе ,Т3 =42,5 Нм (см. табл.1). Подставив значения в формулу (3.1) получим:
Принимаем окончательно по ГОСТ6636-69 [4,табл.13.15]
Определяем модуль [2,c.36]:
mn=(0,01…0,02)·70; mn=0,7; Принимаем модуль mn=1мм [2,c.36] Так как тихоходная ступень внутреннего зацепления определяем разность зубьев зубьев по формуле [5,т.2, c.432]: z2-z1=2aw/mn (3,3) z2-z1=2·70/1; z2-z1=140. Определяем число зубьев шестерни и колеса по формулам (3.13) [2,c.37]: z1= z2-z1/(U2+1); z1=140/6=23,3; z1=24; z2= z2-z1-+z1=140+24=164; z2=164. Отклонения передаточного числа от номинального нет. Определяем делительные диаметры шестерни и колеса по формуле [5,т.2, c.432]: d=mn·z; (3.4) d1=mn·z1=1х24=24мм; d2=mn·z2=1х164=164мм; Определяем остальные геометрические параметры шестерни и колеса по формулам [5,т.2, c.432]:
Определяем окружные скорости колес
Назначаем точность изготовления зубчатых колес – 7F [2,c.32]. Определяем силы в зацеплении [4, табл.6.1]: - окружная
Таблица 2 Параметры зубчатой передачи тихоходной ступени
- радиальная
Осевые силы в прямозубой передачи отсутствуют. Все вычисленные параметры заносим в табл.2. 3.2 Проверочный расчет по контактным напряжениям Проверку контактных напряжений производим по формуле {4, c.64]:
где: - К - вспомогательный коэффициент, для прямозубых передач К=436; Ft =531Н (табл.2); U2=5; КНα – коэффициент, учитывающий распределение нагрузки между зубьями, для прямозубых колес КНα =1; КНβ – см. п.3.1; КНυ – коэффициент динамической нагруки, зависящий от окружной скорости колес и степени точности передачи, КНυ =1,04 [4, табл.4.3].
Определяем ∆σН
3.3 Проверочный расчет зубьев на изгиб Расчетные напряжения изгиба в основании ножки зубьев колеса и шестерни [4,с.67]:
где: КFβ – коэффициент неравномерности нагрузки по длине зуба, для прирабатывающихся зубьев КFβ =1; КFv - коэффициент динамической нагруки, зависящий от окружной скорости колес и степени точности передачи, КНυ =1,1 [4, табл.4.3]; YF1 и YF2 – коэффициенты формы зуба шестерни и колеса, YF1 =3,9, YF2 =3,61 [4,табл.4.4]. Подставив значения в формулы (3.11) и (3.12), получим:
Прочность зубьев на изгиб обеспечивается. Определяем ∆σF
Все вычисленные параметры проверочных расчетов заносим в табл.3. Таблица 3 Параметры проверочных расчетов
4 Расчет быстроходной ступени привода Межосевое расстояние для быстроходной ступени с учетом того, что редуктор соосный и двухпоточный, определяем половину расстояния тихоходной ступени: а=d2-d1; а=84-14=70мм. Из условия (3.2) принимаем модуль mn=1,5мм Определяем суммарное число зубьев по формуле (3.12) [1,c.36]: zΣ=2а/mn; zΣ=2·70/1,5; zΣ=93,3 Принимаем zΣ=94. Определяем число зубьев шестерни и колеса по формулам (3.13) [2,c.37]: z1= zΣ/(U1+1); z1=94/(2,5+1); z1=26,1; принимаем z1=26. Тогда z2= zΣ-z1=94-26=68 Фактическое передаточное соотношение U1=68/26=2,6 Отклонение передаточного числа от номинального незначительное. Определяем делительные диаметры шестерни и колеса по формуле (3.17) [2,c.37]: d1=mn·z1=1,5х26=39мм; d2=mn·z2=1,5х68=102мм; Определяем остальные геометрические параметры шестерни и колеса по формулам [2,c.37]:
Определяем окружные скорости колес
Назначаем точность изготовления зубчатых колес – 7А [2,c.32]. Определяем силы в зацеплении (3.7, 3.8): - окружная
- радиальная Осевые силы в прямозубой передачи отсутствуют. Все вычисленные параметры заносим в табл.4. Таблица 4 Параметры зубчатой передачи быстроходной ступени
Учитывая, что геометрические параметры быстроходной ступени незначительно отличаются от тихоходной, выполнение проверочных расчетов нецелесообразно. 5 Проектный расчет валов редуктора По кинематической схеме привода составляем схему усилий, действующих на валы редуктора по закону равенства действия и противодействия. Для этого мысленно расцепим шестерни и колеса редуктора, при этом дублирующий вал не учитываем. Схема усилий приведена на рис.1.
Рис.2 Схема усилий, действующих на валы редуктора. Из табл.1,2,4 выбираем рассчитанные значения: Т1=3,4 Нм; Т2=8,5 Нм; Т3=42,5 Нм; Ft1=166,7 Н; Ft2=1012 Н; Fr1=60,7 Н; Fr2=368 Н; d1=39мм; d2=102мм; d3=14мм; d4=84мм. Fm1 и Fm1 – консольные силы от муфт, которые равны [4, табл.6.2]:
Rx и Ry – реакции опор, которые необходимо рассчитать. Так как размеры промежуточного вала определяются размерами остальных валов, расчет начнем с тихоходного вала. 5.1 Расчет тихоходного вала редуктора Схема усилий действующих на валы редуктора представлена на рис.2. Назначаем материал вала. Принимаем сталь 40Х, для которой [2,
табл.8.4] σв=730Н/мм2; Определяем диаметр выходного конца вала под полумуфтой из расчёта на чистое кручение [2,c.161]:
где [τк]=(20…25)МПа Принимаем [τк]=20МПа. Принимаем окончательно с учетом стандартного ряда размеров Rа20 (ГОСТ6636-69):
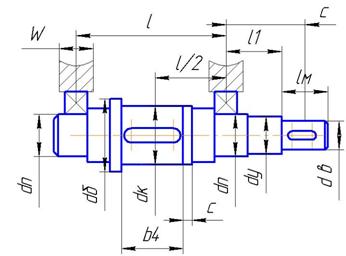
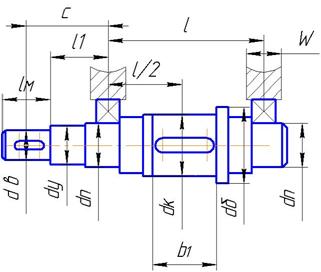
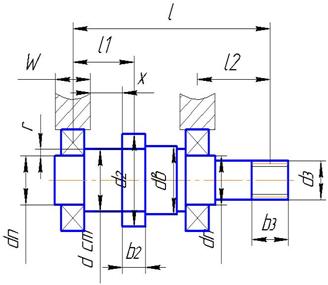
Намечаем приближенную конструкцию ведомого вала редуктора (рис.3), увеличивая диаметр ступеней вала на 5…6мм, под уплотнение допускается на 2…4мм и под буртик на 10мм. Рис.3 Приближенная конструкция тихоходного вала
b4=25мм. Учитывая, что осевых нагрузок на валу
нет предварительно назначаем подшипники шариковые радиальные однорядные особо легкой
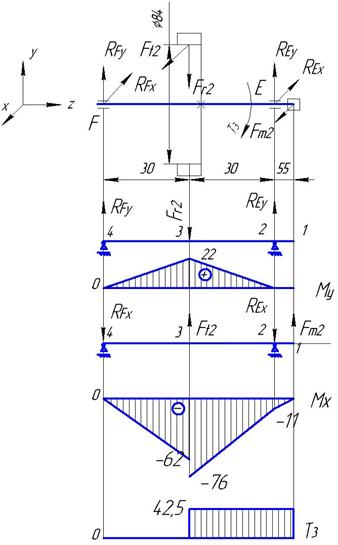
серии по Выбираем конструктивно остальные размеры: W=20мм; lм=20мм; l1=35мм; l=60мм; с=5мм. Определим размеры для расчетов: l/2=30мм; с=W/2+ l1+ lм/2=55мм – расстояние от оси полумуфты до оси подшипника. Проводим расчет тихоходного вала на изгиб с кручением. Заменяем вал балкой на опорах в местах подшипников (см. рис.4). Назначаем характерные точки 1,2, 3 и 4. Определяем реакции в подшипниках в вертикальной плоскости. ΣМ2y=0; RFy·0,06-Fr2·0,03=0 RFy= 368·0,06/ 0,03; RЕy= RFy=736Н.
Рис.4 Эпюры изгибающих моментов тихоходного вала Определяем изгибающие моменты в характерных точках: М1у=0; М2у=0; М3у= RЕy·0,03; М3у =22Нм2; М3у=0; Строим эпюру изгибающих моментов Му, Нм2 (рис.3) Определяем реакции в подшипниках в горизонтальной плоскости. ΣМ4x=0; Fm2·0,115- RЕx·0,06+ Ft2·0,03=0; RЕx=( 814·0,115+ 1012·0,03)/ 0,06; RЕx=2066Н; ΣМ2x=0; Fm2·0,055- Ft2·0,03+ RFx·0,6=0; RFx= (1012·0,03- 814·0,055)/ 0,06; RFx=-240Н, результат получился отрицательным, следовательно нужно изменить направление реакции. Определяем изгибающие моменты: М1х=0; М2= -Fr2·0,03 М2х=-368·0,03; М2х=-11Нм; М3хслева=-Fm2·0,085-RЕх ·0,055; М3хслева==-814·0,085-240 ·0,03; М3хслева=-76Нм; М3х=- REх ·0,055; М3х=- 2066 ·0,03; М3х=- 62; М4х=0; Строим эпюру изгибающих моментов Мх. Крутящий момент Т1-1= Т2-2= Т3-3= T3=42,5Нм; T4-4=0. Определяем суммарные радиальные реакции [4,рис 8.2]:
Определяем результирующий изгибающий момент в наиболее опасном сечении (в точке 3) [4,рис 8.2]:
Эквивалентный момент:
5.2 Расчет быстроходного вала редуктора Схема усилий, действующих на быстроходный вал представлена на рис.2. Назначаем материал вала. Принимаем
сталь 40Х, для которой [2, табл.8.4] σв=730Н/мм2;
Определяем диаметр выходного конца вала под полумуфтой из расчёта на чистое кручение [2,c.161]:
где [τк]=(20…25)Мпа Принимаем [τк]=20Мпа.
Принимаем окончательно с учетом стандартного ряда размеров Rа5 (ГОСТ6636-69):
Намечаем приближенную конструкцию быстроходного вала вала редуктора (рис.5), увеличивая диаметр ступеней вала на 5…6мм, под уплотнение допускается на 2…4мм и под буртик на 10мм.
b1=22мм. Учитывая,
что осевых нагрузок на валу нет предварительно назначаем подшипники шариковые
радиальные однорядные особо легкой серии по Выбираем конструктивно остальные размеры: W=14мм; lм=16мм; l1=25мм; l=60мм. Определим размеры для расчетов: l/2=30мм; с=W/2+ l1+ lм/2=40мм – расстояние от оси полумуфты до оси подшипника. Проводим расчет быстроходного вала на изгиб с кручением. Рис.5 Приближенная конструкция быстроходного вала Заменяем вал балкой на опорах в местах подшипников (см. рис.6). Назначаем характерные точки 1,2, 3 и 4. Определяем реакции в подшипниках в вертикальной плоскости. ΣМ2y=0; RАy·0,06-Fr1·0,03=0 RАy= 60,7·0,06/ 0,03; RАy= RВy=121Н. Определяем изгибающие моменты в характерных точках: М1у=0; М2у=0; М3у= RАy·0,03; М3у =3,6Нм2; М3у=0; Строим эпюру изгибающих моментов Му, Нм2 (рис.6). Определяем реакции в подшипниках в горизонтальной плоскости. ΣМ4x=0; Fm1·0,1- RАx·0,06+ Ft1·0,03=0; RАx= (130·0,1+ 166,7·0,03)/ 0,06; RАx=300Н;
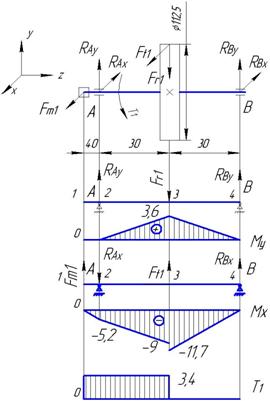
Рис.6 Эпюры изгибающих моментов быстроходного вала ΣМ2x=0; Fm1·0,02- Ft1·0,03+ RВx·0,06=0; RВx= (166,7·0,03- 130·0,02)/ 0,06; RВx=40Н Определяем изгибающие моменты: М1х=0; М2= -Fm2·0,04 М2х=-130·0,04; М2х=-5,2Нм; М3хсправа=-Fm1·0,1+RВх ·0,03; М3хсправа==-130·0,1+40 ·0,03; М3хсправа=-11,7Нм; М3х=- RАх ·0,03; М3х=- 300 ·0,03; М3х=- 9; М4х=0; Строим эпюру изгибающих моментов Мх. Крутящий момент Т1-1= Т2-2= Т3-3= T3=3,4Нм; T4-4=0. Определяем суммарные радиальные реакции [4,рис 8.2]:
Определяем результирующий изгибающий момент в наиболее опасном сечении (в точке 3) [4,рис 8.2]:
Эквивалентный момент:
5.3 Расчет промежуточного вала Назначаем материал вала. Принимаем
сталь 40Х, для которой [1, табл.8.4] σв=730Н/мм2;
Определяем диаметр выходного конца вала из расчёта на чистое кручение
где [τк]=(20…25)Мпа [1,c.161] Принимаем [τк]=20Мпа.
С учетом того, что выходной конец промежуточного вала является валом-шестерней с диаметром выступов 24мм, принимаем диаметр вала под подшипник 25мм.
Намечаем приближенную конструкцию промежуточного вала редуктора (рис.7), увеличивая диаметр ступеней вала на 5…6мм
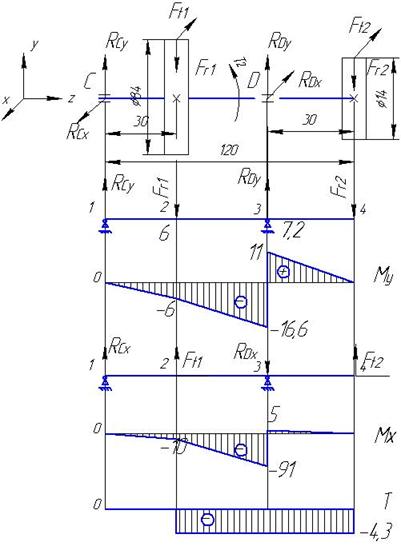
Рис.7 Приближенная конструкция промежуточного вала dст=30мм; х=8мм; W=20мм; r=2,5мм; dв=28мм. Расстояние l определяем из суммарных расстояний тихоходного и быстроходного валов с зазором между ними 25…35мм. l=60+30+30=120мм. l1=30мм; l2=30мм. Предварительно назначаем подшипники шариковые радиальные однорядные особо легкой серии по dп=25мм подшипник №105, у которого Dп=47мм; Вп=12мм [4, табл.К27]. Заменяем вал балкой на опорах в местах подшипников. Рассматриваем вертикальную плоскость (ось у) Определяем реакции в подшипниках в вертикальной плоскости. åМСу=0; -RDу·0,09+Fr1·0,03+Fr2·0,12=0 RDy=(368·0,03+60,7·0,12)/ 0,09; RDy==204Н. åМDу=0; RCy·0,09- Fr1·0,06+ Fr2·0,03=0; RCy=(368·0,06-60,7·0,03)/ 0,09; RCy=225Н. Назначаем характерные точки 1, 2, 3, и 4 и определяем в них изгибающие моменты: М1у=0; М2у=-RCy·0,03; М2у=-6Нм; М3услева=-RCy·0,09+Fr1·0,06; М3услева=-16,6Нм М3усправа= Fr2·0,03; М3усправа= 11 М4у=0; Строим эпюру изгибающих моментов Му, Нм (рис.8). Определяем реакции в подшипниках в горизонтальной плоскости. åМСх=0; RDx·0,09-Ft1·0,03-Ft2·0,12=0; RDx=( 166,7·0,03+ 1012·0,12)/0,09; RDx=1404Н; åМDх=0; RCx·0,09+ Ft1·0,06-Ft2·0,03=0; RCx=(1012·0,03+166,7·0,06)/ 0,09; RCx=337Н. Назначаем характерные точки 1, 2, 3 и 4 и определяем в них изгибающие моменты: М1x=0; М2x=-RCx·0,03; М2x=-10Нм; М3xслева= -RCx·0,09-Ft1·0,06; М3xслева=-91Нм; М3xсправа= Ft2·0,03; М3xсправа=5Нм; М4у=0. Строим эпюру изгибающих моментов Му, Нм (рис.8)
Рис.8 Эпюры изгибающих и крутящих моментов промежуточного вала. Крутящий момент Т1-1=0; Т2-2=-Т3-3=- T2/2=-4,3Нм; Т4-4=0. Определяем суммарные радиальные реакции [4,рис 8.2]:
Определяем результирующий изгибающий момент в наиболее опасном сечении (в точке 3) [4,рис 8.2]:
Эквивалентный момент:
Все рассчитанные значения сводим в табл.5. Таблица 5 Параметры валов
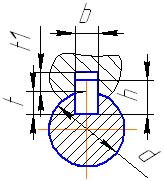
6 Подбор и проверочный расчет шпонок Выбор и проверочный расчет шпоночных соединений проводим по [4]. Обозначения используемых размеров приведены на рис.11.
Рис.9 Сечение вала по шпонке 6.1 Шпонки быстроходного вала Для выходного конца быстроходного вала при d=10 мм подбираем призматическую шпонку со скругленными торцами по ГОСТ23360-78 bxh=3x3 мм2 при t=1,8мм (рис.9). При длине ступицы полумуфты lм=16 мм выбираем длину шпонки l=14мм. Материал шпонки – сталь 40Х нормализованная. Напряжения смятия и условия прочности определяем по формуле:
где Т – передаваемый момент, Н×мм; Т1=3,4 Н×м. lр – рабочая длина шпонки, при скругленных концах lр=l-b,мм; [s]см – допускаемое напряжение смятия. С учетом того, что на выходном конце быстроходного вала устанавливается полумуфта из ст.3 ([s]см=110…190 Н/мм2) вычисляем:
Условие выполняется.
6.2 Шпонки промежуточного вала Для зубчатого колеса вала при d=30 мм подбираем призматическую шпонку со скругленными торцами bxh=8x7 мм2 при t=4мм, t1=3,3мм. Т2=8,5Нм. При длине ступицы шестерни lш=25 мм выбираем длину шпонки l=25мм. Материал шпонки – сталь 45 нормализованная. Проверяем напряжение смятия, подставив значения в формулу (6.1):
Условие выполняется. 6.3 Шпонки тихоходного вала Передаваемый момент Т3=42,5Нм. Для выходного конца вала при d= 22мм подбираем призматическую шпонку со скругленными торцами bxh=6x6 мм2 при t=3,5мм. При длине ступицы полумуфты lМ=20 мм выбираем длину шпонки l=16мм.
Для зубчатого колеса тихоходного вала при d=35 мм подбираем призматическую шпонку со скругленными торцами bxh=10x8мм2 при t=5мм. При длине ступицы шестерни lш=20 мм выбираем длину шпонки l=20мм. С учетом того, что на ведомом валу устанавливаются шестерни из стали 45 ([s]см=170…190 Н/мм2) вычисляем по формуле (6.1):
условие выполняется. Таблица 6 Параметры шпонок и шпоночных соединений
7 Проверочный расчет валов на статическую прочность В соответствии с табл.5 наиболее опасным является сечение 3-3 тихоходного вала, в котором имеются концентраторы напряжений от посадки зубчатого колеса с натягом, шпоночного паза и возникают наибольшие моменты. Исходные данные для расчета: МИэкв= 89Нм; МИ=79Нм; Т3-3=42,5Нм; dв=35мм; в=10мм – ширина шпонки, t=5мм – глубина шпоночного паза, l=22мм – длина шпонки. При расчете принимаем, что напряжения изгиба изменяются по симметричному циклу, а напряжения кручения – по отнулевому циклу. Определяем диаметр вала в рассчитываемом сечении при допускаемом напряжении при изгибе [σ-1]и=60МПа:
Условие соблюдается. Определяем напряжения изгиба: σи=Ми/W; где W – момент сопротивлению изгибу. По [4,табл.11.1]:
σи=79000/3566=22Н/мм2. При симметричном цикле его амплитуда равна: σа= σи =22Н/мм2. Определяем напряжения кручения: τк=Т3-3/Wк; где Wк – момент сопротивлению кручению. По [4,табл.22.1]:
τк=42500/7775=5,4Н/мм2. При отнулевом цикле касательных напряжений амплитуда цикла равна: τа= τк /2=5,4/2=2,7Н/мм2. Определяем коэффициенты концентрации напряжении вала [4, с.258]: (Кσ)D=( Кσ/Кd+ КF-1)/ Кy; (Кτ)D=( Кτ/Кd+ КF-1)/ Кy; (7.1) где Кσ и Кτ – эффективные коэффициенты концентрации напряжений, по табл.11.2 [4] выбираем для шпоночных пазов, выполненных концевой фрезой Кσ =1,6, Кτ =1,4; Кd – коэффициент влияния абсолютных размеров поперечного сечения, по табл.11.3 [4] выбираем Кd =0,75; КF- коэффициент влияния шероховатости, по табл.11.4 [4] выбираем для шероховатости Rа=1,6 КF=1,05; Кy - коэффициент влияния поверхностного упрочнения, по табл.11.4 [4] выбираем для закалки с нагревом ТВЧ Кy =1,5. Подставив значения в формулы (7.1) получим: (Кσ)D=( 1,6/0,75+ 1,05-1)/ 1,5=1,45; (Кτ)D=( 1,4/0,75+ 1,05-1)/ 1,5=1,28. Определяем пределы выносливости вала [4, c263]: (σ-1)D=σ-1/(Кσ)D; (τ-1)D=τ-1/(Кτ)D; (7.2) где σ-1 и τ-1 – пределы выносливости гладких образцов при симметричном цикле изгиба и кручения, по табл.3. [4] σ-1 = 380Н/мм2 , τ-1 ≈0,58 σ-1 =220Н/мм2; (σ-1)D=380/1,45=262Н/мм2; (τ-1)D=220/1,28=172 Н/мм2. Определяем коэффициенты запаса прочности по нормальным и касательным напряжениям 4, c263]: sσ=(σ-1)D/ σа; sτ=(τ-1)D/ τа. (7.3) sσ=262/ 22=12; sτ=172/ 2,7=63,7. Определяем общий коэффициент запаса по нормальным и касательным напряжениям [4, c263]:
где [s]=1,6…2,1 – допускаемый коэффициент запаса прочности.
Сопротивление усталости вала в сечении 3-3 обеспечивается, расчет остальных валов не проводим, т.к. расчет проведен на самом опасном сечении, и коэффициент запаса прочности значительно превышает допустимый. 8 Выбор и проверочный расчет подшипников Предварительно выбранные подшипниками с действующими на них радиальными нагрузками приведены в табл.7. Таблица 7 Параметры выбранных подшипников
Подшипники устанавливаем по схеме «враспор». Пригодность подшипников определяем по условиям [4, c.129]: Ср≤С; Lр≥Lh; где Ср – расчетная динамическая грузоподъемность; Lh – требуемая долговечность подшипника, для зубчатых редукторов Lh =10000ч.
где ω – угловая скорость соответствующего вала (см. табл.1); m=3 для шариковых подшипников; RЕ – эквивалентная динамическая нагрузка, при отсутствии осевых усилий [4, табл.9.1]: RЕ=V×RАКδКτ (8.2) где Kd - коэффициент безопасности; Kd =1,1…1,2 [4, табл.9.4]. Принимаем Kd =1,1. V – коэффициент вращения, при вращении внутреннего кольца V=1 Kτ – температурный коэффициент; Kτ =1 (до 100ºС) [4, табл.9.4]. Определяем расчетную долговечность подшипников в часах [4, c.129]:
Подставив значения в формулы (8.1)-(8.3) проверяем подшипники. Для быстроходного вала: RЕ=323х1,1=355Н;
Для промежуточного вала: RЕ=1419х1,1=1560Н;
Для тихоходного вала: RЕ=2118х1,1=2330Н;
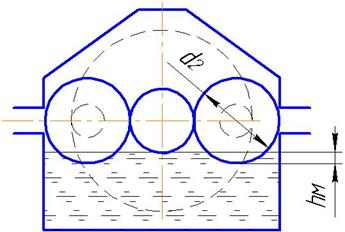
Окончательные параметры подшипников приведены в табл.7. Параметры выбранных подшипников 9 Выбор масла, смазочных устройств Используем картерную систему смазывания. В корпус редуктора заливаем масло так, чтобы венец зубчатого колеса был в него погружен на глубину hм (рис.10): hм max £ 0.25d2 = 0.25×102 = 25,5мм; hм min = 2×m = 2×1,5 = 3мм. При вращении колеса масло будет увлекаться его зубьями, разбрызгиваться, попадать на внутренние стенки корпуса, откуда стекать в нижнюю его часть. Внутри корпуса образуется взвесь частиц масла в воздухе, которым покрываются поверхности расположенных внутри корпуса деталей, в том числе и подшипники.
Рис.10 Схема определения уровня масла в редукторе Объем масляной ванны принимаем из расчета 0,5 л на 1кВт передаваемой мощности V = 0,5×Nдв = 0,5×0,25 = 0,125 л. Контроль уровня масла производится жезловым маслоуказателем, который ввинчивается в корпус редуктора при помощи резьбы. Для слива масла предусмотрена сливная пробка. Заливка масла в редуктор производится через съемную крышку в верхней части корпуса. Выбираем смазочный материал. Для этого ориентировочно рассчитаем необходимую вязкость:
где ν50 – рекомендуемая кинематическая вязкость смазки при температуре 50°С; ν1 =170мм2/с – рекомендуемая вязкость при v=1м/с для зубчатых передач с зубьями без термообработки; v=1,2м/с – окружная скорость в зацеплении
Принимаем по табл.10.29 [4] масло И-220А. И для шестерни, и для зубчатого колеса выберем манжетные уплотнения типа 1 из ряда 1 по ГОСТ 8752-79. Установим их рабочей кромкой внутрь корпуса так, чтобы обеспечить к ней хороший доступ масла. Список использованной литературы 1. Основы конструирования: Методические указания к курсовому проектированию/ Сост. А.А.Скороходов, В.А Скорых.-СПб.:СПбГУКиТ, 1999. 2. Дунаев П.Ф., Детали машин, Курсовое проектирование. М.: Высшая школа, 1990. 3. Скойбеда А.Т., Кузьмин А.В., Макейчик Н.Н., Детали машин и основы конструирования, Минск: «Вышейшая школа», 2000. 4. Шейнблит А.Е. Курсовое проектирование деталей машин: Учеб. пособие. – М.: Высш. шк., 1991 5. Анурьев В.И. Справочник конструктора-машиностроителя: В 3 т. -8-е изд. перераб. и доп. Под ред. И.Н. Жестковой. – М.: Машиностроение, 1999 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
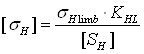 (2.1)
(2.1)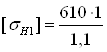 ;
; 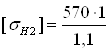 ;
; 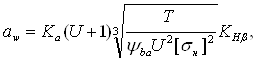 (3.1)
(3.1)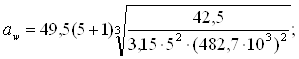
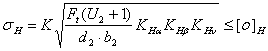 ; (3.9)
; (3.9)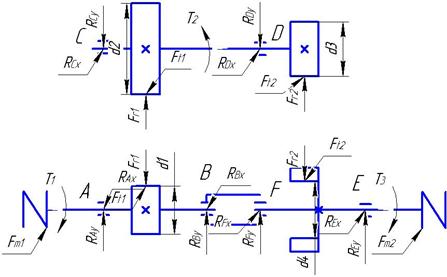
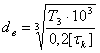
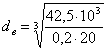 ;
; 
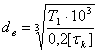
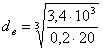 ;
; 
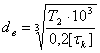 ;
;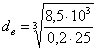 ;
; 
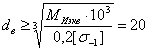 мм; 35>20.
мм; 35>20.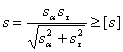 (7.4)
(7.4)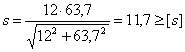
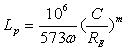 (8.3)
(8.3)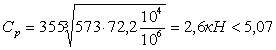 -
условие выполняется;
-
условие выполняется;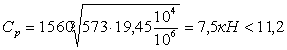 - условие выполняется;
- условие выполняется;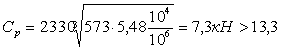 - условие выполняется.
- условие выполняется.