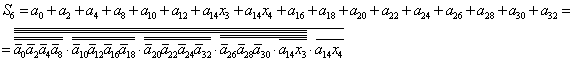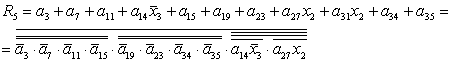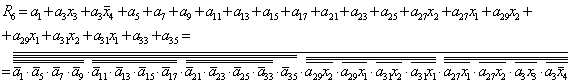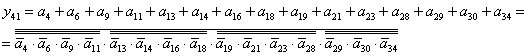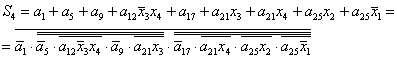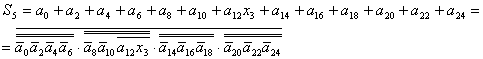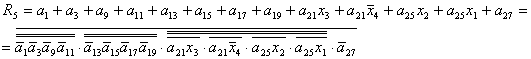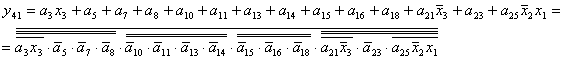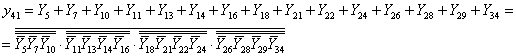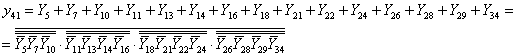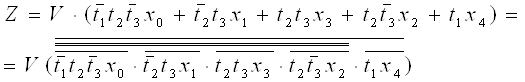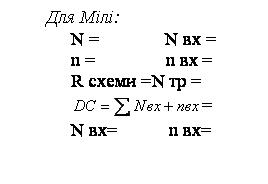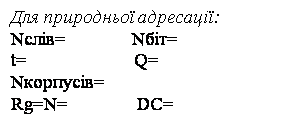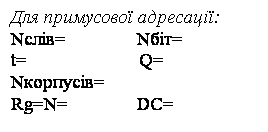Курсовая работа: Синтез керуючих автоматівКурсовая работа: Синтез керуючих автоматівВСТУП Принцип мікропрограмного керування припускає, що цифровий пристрій складається з двох частин: операційний автомат (ОА) і керуючий автомат (КА). ОА виконує найпростіші операції (мікрооперації) типу зсув, алгебраїчне додавання, кон’юнкція, диз’юнкція і т.п. КА формує послідовність керуючих символів в ОА, під впливом яких ОА реалізує більш складні алгоритми. Такі послідовності операцій називаються мікропрограмами та, звичайно, записуються у вигляді граф-схеми алгоритму. КА розділяються на дві великі групи: автомати з жорсткою логікою та автомати з програмованою логікою. У свою чергу автомати з жорсткою логікою підрозділяються на автомати, виконані за схемою Мілі (КА Мілі) і за схемою Мура (КА Мура), автомати з програмованою логікою – на автомати з примусовою адресацією та з природною адресацією. В автоматах з жорсткою логікою схема автомата однозначно інтерпретує граф-схему мікропрограми. В автоматах із програмованою логікою граф-схема інтерпретується у вигляді програми, що зберігається в пам’яті автомата. 1. СИНТЕЗ ОПЕРАЦІЙНОГО АВТОМАТА 1.1 Аналіз вхідних даних
Загальна формула для обчислювання результату S має такий вигляд:
Формулі
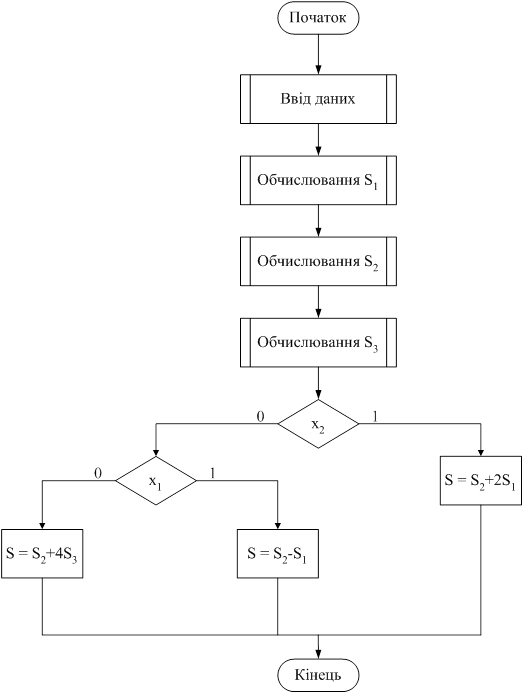
Загальний алгоритм для обчислювання формули S приведений на рисунку 1.1. Для обчислювання формули S використовується ІМp-модель (Individual Mutual with Parallel part - IMp).
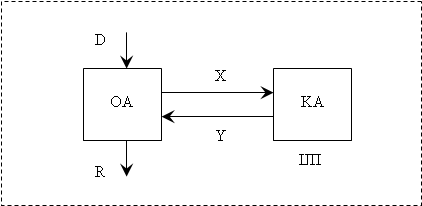
Рис. 1.1 – Загальний алгоритм для обчислювання формули S Схему взаємодії операційного та керуючої частин у цифровому просторі зображено на рисунку 1.2.
Рис. 1.2 – Структура цифрового пристрою Структурна схема ІМp - моделі зображена на рисунку 1.3
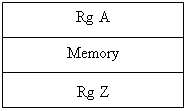
Рис. 1.3 – Структура операційного пристрою Пам’ять автомата складається з регістрів загального призначення R1, ... , Rn. Локальні шини А1, А2, A3 призначені для прийому інформації з пам’яті та передачі її на комбінаційні схеми (КС). В даному випадку використовуються КС двох типів: одномісні та двомісні.
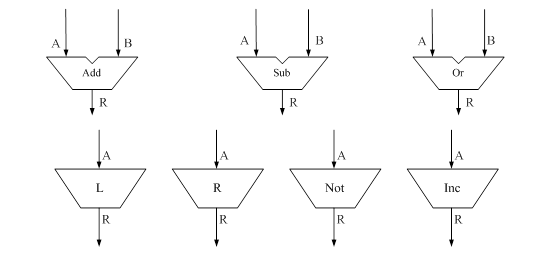
Рис. 1.4 – Приклад комбінаційних схем Однак, у даному ОА використовуються лише деякі з них.
1.2 Розробка функціонального алгоритму Функціональна і структурна організація операційних пристроїв (ОУ) базується на принципі мікро програмного керування, сформульованому в 1951 році М. Уилксом. Відповідно до цього принципу будь-яка машинна операція розділяється на послідовність елементарних дій по обробці інформації – мікро операцій (МО). Порядок проходження мікро операцій визначається спеціальними логічними умовами (ЛУ), що у залежності від значень оброблюваної інформації приймають значення "істина" (1) або "неправда" (0). Алгоритм операцій в ОУ, записаний у термінах мікро операцій і логічних умов, що відбиває порядок проходження мікро операцій у часі, називається мікропрограмою. Функція УА – це оперативна схема алгоритму, операторами якої є символи
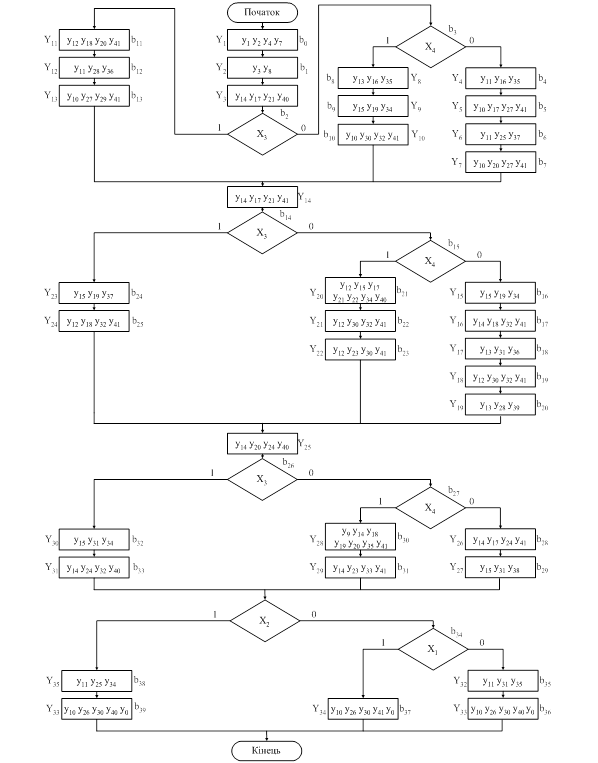
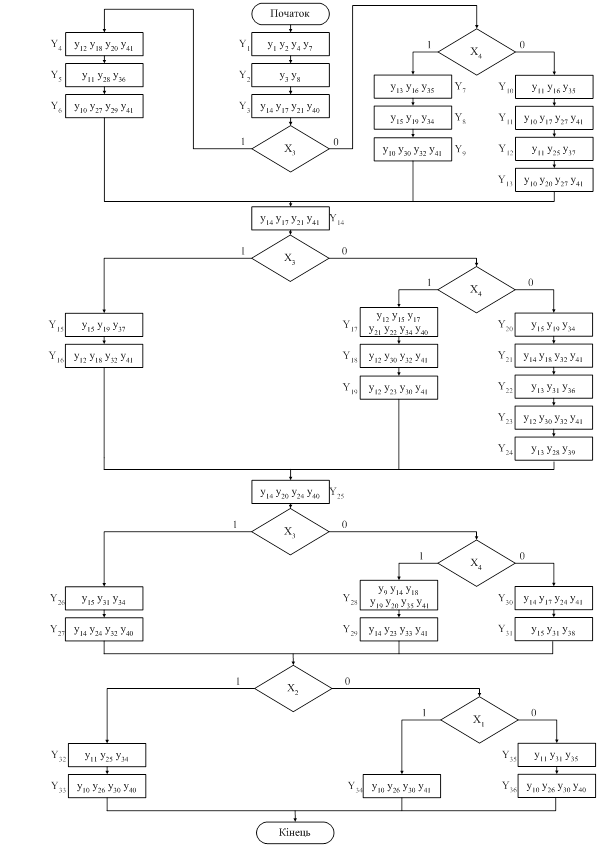
Граф-схема алгоритму. Орієнтований зв'язаний граф – граф, що містить одну початкову вершину, одну кінцеву вершину, довільну безліч умовних і операторних вершин. Будова ІМр автомата дозволяє паралельно виконувати одномісну та двумісну операції, тобто можливо виконувати за одне завантаження автомату завантаження двох операнд. Наприклад, у п’ятій вершині зроблено саме так. Кожній дії, завантаженню автомата, відповідає Y[і]. Ідентичні дії відповідають однаковим командам, Y[і]. Логічні умови позначаються – XL, однаковим умовам відповідають однакові XL. Функціональний алгоритм приведений на рисунку 1.5.
Рис. 1.5 – Функціональний алгоритм 1.3 Розробка структурної схеми автомата
1.3.1. Визначення набору регістрів пам’яті: Rg : {RA, RB, RC, RS1, RS2, RS3}
1.3.2. Набір комбінаційних схем: Одномісні: КС1 : {L1, L2, L3, R1, R2, R3} На шину C повинні поступати всі аргументи одномісних операцій. Двомісні: КС2: {Sum, Sub} Припустимо, що операція відіймання виконується наступним чином: Sub := B - A, тому від’ємне завжди повинно знаходитись на шині B, а від’ємник на шині А. В іншій двомісній операції Sum порядок операндів значення не має.
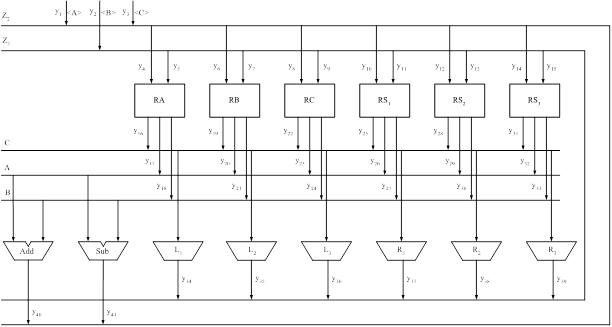
Рис. 1.6 – Структурна схема автомата
1.3.3. Зв'язки між регістрами та локальними шинами Наша схема має три шини: А та B – двомісні, та шина C – одномісна. A {RA, RB, RC, RS1, RS2, RS3} B {RA, RB, RC, RS1, RS2, RS3} C {RA, RB, RC, RS1, RS2, RS3} 1.3.4. Зворотні зв'язки шин Z1 та Z2 з регістрами пам’яті Шини, що є результативними: Z1 – результати одномісних операцій, а Z2 – двомісних операцій. Z1 {RA, RB, RC, RS1, RS2, RS3} Z2 {RA, RB, RC, RS1, RS2, RS3} Кожний елемент, котрий діє у схемі може виконуватись тільки при наявності відповідного керуючого сигналу y[n]. у1, у2, у3 – завантаження початкових даних на шини. у4 – у15 – завантаження даних у регістри пам'яті. у16–у33 – завантаження з пам'яті на локальні шини А, B, C. у34, у39 – завантаження результатів одномісних операцій на шину Z1. y40–у41 – завантаження результатів двомісних операцій на шину Z2. Отримані таким чином дані заносимо до таблиці 1.1 Табл. 1.1 –Таблиця мікрооперацій
Рис. 1.7 – Структурна граф-схема операційного автомата 2. СИНТЕЗ КЕРУЮЧИХ АВТОМАТІВ З ЖОРСТКОЮ ЛОГІКОЮ На практиці використовуються дві моделі МПА - автомат Милі й автомат Мура, розходження між якими полягає у функції виходу. В автоматі Милі вихідний сигнал залежить від поточного стану і вхідного сигналу, а в автоматі Мура‑ тільки від стану. Незалежно від типу МПА для їхнього синтезу використовується однакова методика, що включає наступні етапи: 1. Оцінка станів автомата на ГСА. 2. Побудова таблиці переходів. 3. Кодування станів УА. 4. Побудова прямої структурної таблиці. 5. Формування системи булевських функцій (СБФ) для вихідних сигналів і функцій збудження елементів пам'яті 6. Синтез схеми в заданому елементному базисі.
2.1 Методика синтезу автомата Мура
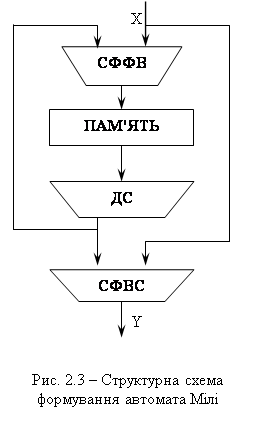
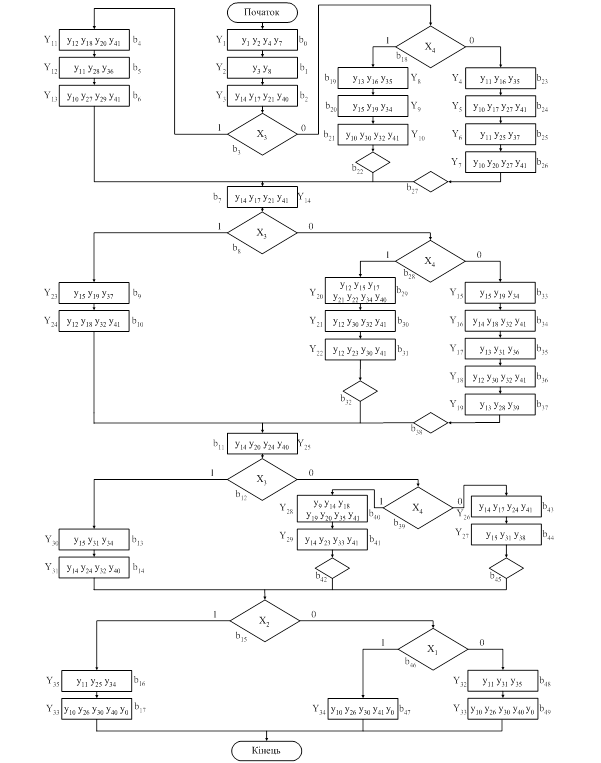
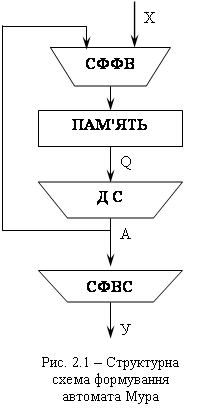
Побудова таблиці переходів зводиться, до формувань по відзначеної ГСА таблиці, що містить стовпці: am - вихідний стан; as - стан переходу; X(am, as) - кон’юнкція вхідних перемінних, визначальний перехід (am, as) і відповідна функції переходу іj, де Yі відзначений станом am, Y – стан As, Y(am) - вихідні сигнали; h=1, H - номер переходу. При кодуванні станів необхідно прагнути до такого кодування, що зменшує кількість функцій збудження, що приймають одиничне значення, і, отже, складність схеми УА. Для цих цілей рекомендується використовувати алгоритми кодування. Структурна схема автомата Мура (див. рис. 2.1): 1. Пам'ять – зберігає код стану (Q); 2. Дешифратор (ДС) – виконує перетворення коду в унітарний код, вказує на поточний стан. На базі вектора станів А схема вихідних сигналів (СФВС) формує вихідні сигнали керуючого автомата y. Автомат Мура має свою відмінність - вихідний сигнал y залежить не від вхідного Х, а від стану. Автомат Мура, як і кожний інший автомат складається з двох частин: комбінаційна схема та пам'ять (тригер). Для синтезу
автомата Мура потрібно позначити кожну операторну вершину через a[i], починаючи з “початок” - Записуємо до таблиці 2.2 отримані результати: поточний стан (мітка вершини та номер її значення в двійковій системі вираховування), наступний стан (мітка вершини та номер її значення в двійковій системі вираховування), вхідний сигнал Х, вихідний сигнал Y та функції збудження пам'яті у заданому тригері (згідно варіанта - у тригері RS).
Табл. 2.1 – Структура переходів для автомата Мура
2.2 Формування схеми автомата Мура
2.2.1 Функції збудження пам'яті та їх синтез у заданий базис:
2.2.2 Синтез дешифратора та його синтез у заданий базис: Синтез дешифратора для автомата Мура розробляється так само, як і синтез для автомата Мілі(див. далі).
2.2.3 Рівняння вихідних сигналів та їх синтез у заданий базис:
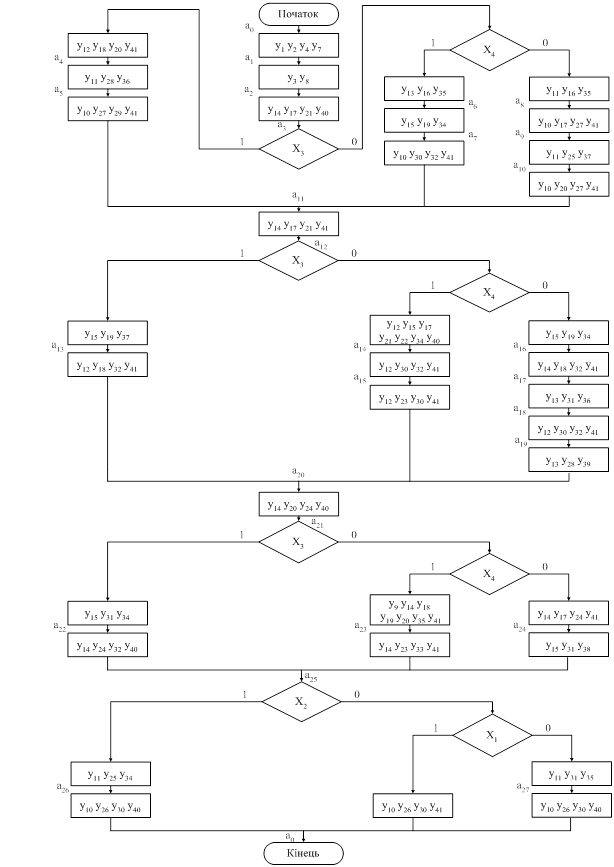
2.3 Методика синтезу автомата Мілі Структурна схема автомата Мілі (зображена на рис. 2.3) включає ті ж етапи, що і синтез КА Мура. Відрізняється від схеми автомата Мура тим, що вихідні сигнали Y залежать від вхідних Х. Порядок синтезу автомата Мілі: 1. Позначаємо вхід початкових та кінцевих станів; 2. Позначаємо вихід операторних вершин у паралельних гілках одним станом (див. рис. 2.4). Кожна операторна вершина відзначається окремим станом. Таблиця переходів автомата має наступні стовпці: am, as - вихідний стан і стан переходу. Х (am,as) - кон’юнкція вхідних перемінних, визначальний перехід (am, as), Yh - вихідний сигнал на переході (am, as). Для синтезу логічної схеми в заданому базисі необхідно перетворити СБФ за правилами Де-Моргана з урахуванням обмежень елементного базису - числа входів і навантажувальної здатності.
Рис. 2.5 – Граф-схема автомата Мілі Табл. 2.2 – Структура переходів для автомата Мілі
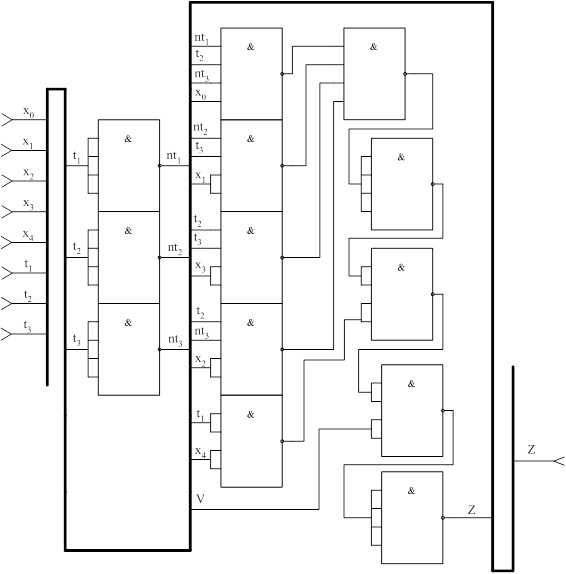
2.4 Формування схеми автомата Мілі
2.4.1 Функції збудження пам'яті та їх синтез у заданий базис:
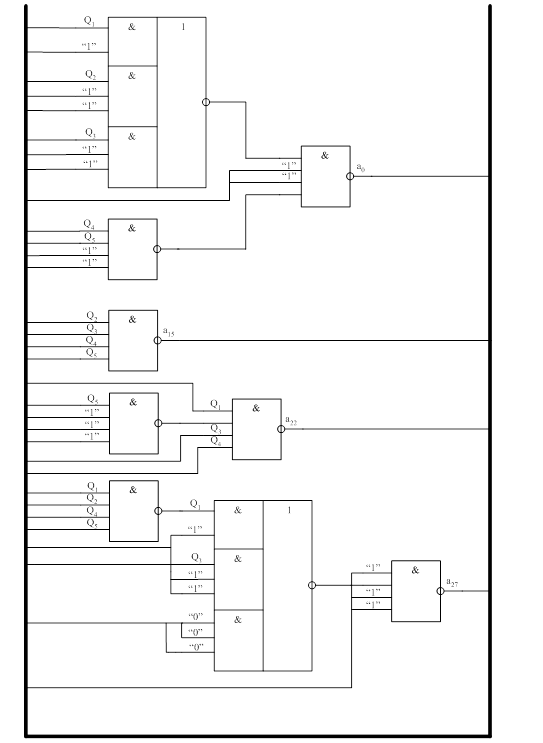
2.4.2 Синтез дешифратора та його синтез у заданий базис. Методика синтезу дешифратора до автомата Мілі: - таблиця істинності (Карта Карно); - Карта Карно для одержання мінімізованої функції збудження; - запис формул функцій збудження; - побудова схеми. Оскільки на кожнім наборі вхідних перемінних активний тільки один біт, то Карту Карно можна зобразити одну загальну для усіх вихідних сигналів. При цьому в осередках Карти Карно записуються не одиниці, а імена відповідних функцій. Табл. 2.3 – Карта Карно до дешифратора автомата Мілі
...
...
...
Електрична схема дешифратора зображена на рисунку 2.6.
Рис. 2.6 – Дешифратор. Функціональна схема. 2.4.3 Рівняння вихідних сигналів та їх синтез у заданий базис:
3. Синтез автоматів з програмованою логікою
3.1 Синтез автомата з примусовою адресацією команд ПЗУ – зберігаємий набір команд, кожна з котрих несе інформацію про набір вихідного сигналу, про поточний такт та адресу мікрокоманд, котрі повинні бути виконані у наступному такті.
Рис. 3.1 - Формат МК
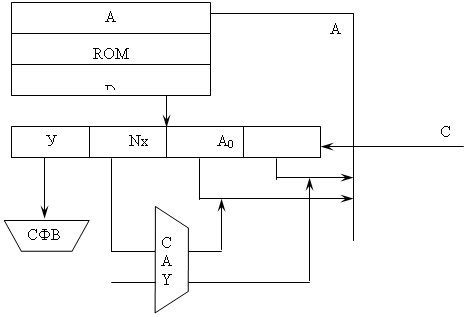
Рис. 3.2 - Структурна схема АПЛ з примусовою адресацією мікрокоманд Аналіз рисунка 3.2: - СФВС - дозволяє декодувати інформацію, що утримується в полі Y. - САХ - являє собою мультиплексор на інформаційні входи якого подаються вхідні сигнали, а на адресні, код з поля Nх при цьому на А0 завжди подається сигнал "0", у такий спосіб формується сигнал Z, що забезпечує передачу на адресний вхід пам'яті А або А0, або А1. Для того щоб сформувати вміст ROM по граф-схемі мікрокоманд необхідно: - відзначити номера мікрокоманд; - закодувати вихідні сигнали і сформувати мікрокоманди по заданому форматі; - сформувати таблицю вмісту ROM.
Рис. 3.3 – Граф-схема автомата з примусовою адресацією команд Для скорочення довжини слова ROM будемо використовувати принцип максимального кодування вихідних сигналів. Табл. 3.1 – Максимальне кодування вихідних сигналів
Табл. 3.2 – Структура переходів для автомата з примусовою адресацією команд
Табл. 3.3 – Таблиця кодів станів автомата з примусовою адресацією команд
Табл. 3.4 – Таблиця вхідних сигналів автомата з примусовою адресацією команд
Рівняння
вихідних сигналів та їх
3.2 Синтез автомата з природною адресацією команд У реальних мікропрограмах часто зустрічаються ситуації, коли маються досить довгі сплетіння операторних вершин. У цьому випадку можлива організація схеми, коли безумовний перехід не задається, а виконується нарощуванням адреси мікрокоманди. Таким чином вдається зменшити довжину мікрокоманди за рахунок формування вихідних сигналів і аналізу вхідних сигналів у різні моменти часу. Для цього в автоматах із природною адресацією використовується два формати мікрокоманд:
- операторна
- умовна
Рис. 3.4 – Структурна схема автомата з природною адресацією Аналіз схеми: У регістрі мікрокоманд зберігатися поточне МК, якщо це операторна МК, то працює схема формування вихідних сигналів і в операційний автомат попадає y. При цьому схема аналізу Х формує Z, що змушує адресу, що зберігається в лічильнику збільшитися на одиницю. Якщо в регістрі МК умовна МК, то вихідний сигнал не формується, а схема аналізу Х формує Z, у залежності від значення Z: якщо Z=1, то до значення лічильника команд додається 1, якщо Z=0, то в лічильник попадає адреса мікрокоманди з поля b. Порядок формування змісту ROM такий же як в автоматі з примусовою адресацією мікрокоманд.
Рис. 3.5 – Граф-схема автомата з природною адресацією команд Табл. 3.5 – Структура переходів для автомата з природною адресацією команд
Табл. 3.6 – Таблиця кодів станів автомата з природною адресацією команд
Табл. 3.7 – Таблиця вхідних сигналів автомата з природною адресацією команд
Рівняння вихідних сигналів та їх синтез у заданий базис:
Синтез мультиплексора Табл. 3.8 – Карта Карно до мультиплексора
4. ПОРІВНЯЛЬНА ХАРАКТЕРИСТИКА АВТОМАТІВ
4.1 Порівняльна характеристика автоматів з жорсткою логікою Розрахуємо усі дані по формулам:
N - кількість великих елементів. Nвх – кількість входів на великі елементи. n – кількість малих елементів. nвх - кількість входів на малі елементи. Nтр – кількість тригерів у схемі
Табл. 4.1 – Таблиця обліку апаратурних витрат автоматів з жорсткою логікою
З таблиці 4.1 видно, що R схеми у Мура менше, але входів на DC більше. Тригерів однакова кількість. 4.2 Порівняльна характеристика автоматів з програмованою логікою
Табл.4.2 Таблиця обліку апаратурних витрат автоматів з програмованою логікою
У автомата з природною адресацією МК більш мінімальні апаратні витрати (корпусів), ніж у автомата з примусовою адресацією. Тригерів однакова кількість. Кількість входів на DC однакова. Комбінаційна
частина у АПЛ з природною адресацією більша, ВИСНОВОК операційний керуючий автомат програмований логіка Виконано курсовий проект з дисципліни „Прикладна теорія цифрових автоматів” на тему „Синтез керуючих автоматів”. Були синтезовані основні типи автоматів з жорсткою та програмованою логікою. Хоча всі приведені автомати справилися з поставленою задачею і в достатній мірі реалізували схему керуючого автомата, але є деякі позитивні і негативні особливості синтезу кожного з автоматів. Наприклад, автомати з жорсткою логікою мають досить велику комбінаційну частину, але вони не потребують елементів ROM, це робить ці автомати дуже оптимальними за ціною затрат. Автомати з програмованою логікою виявились досить складними в розрахунках і реалізації, але це повністю компенсувалось універсальністю та гнучкістю програмування, чого не можна було досягнути на автоматах з жорсткою логікою. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
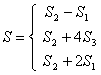
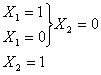
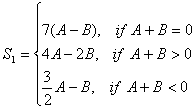
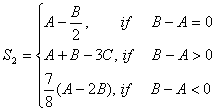
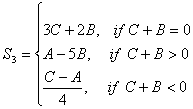

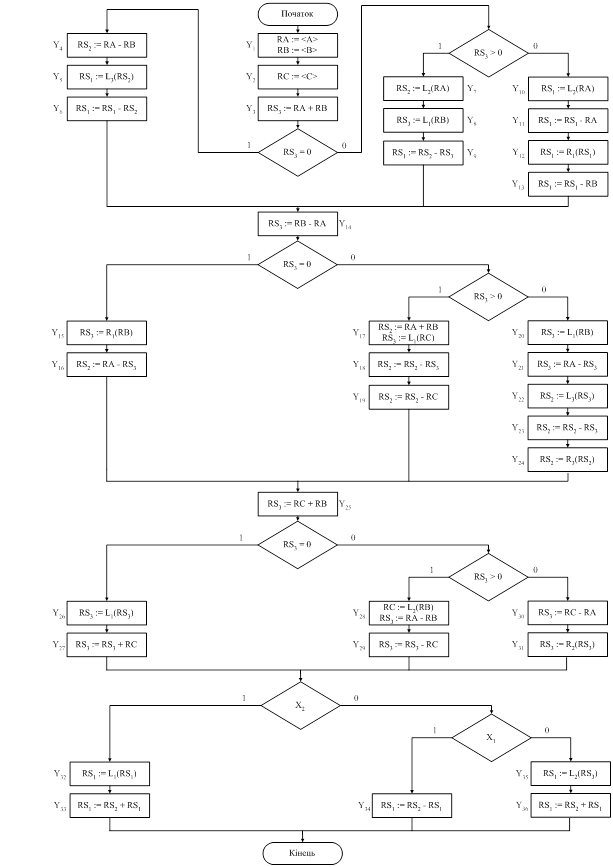
 На першому
етапі початкова і кінцева вершини відзначаються окремим станом.
На першому
етапі початкова і кінцева вершини відзначаються окремим станом.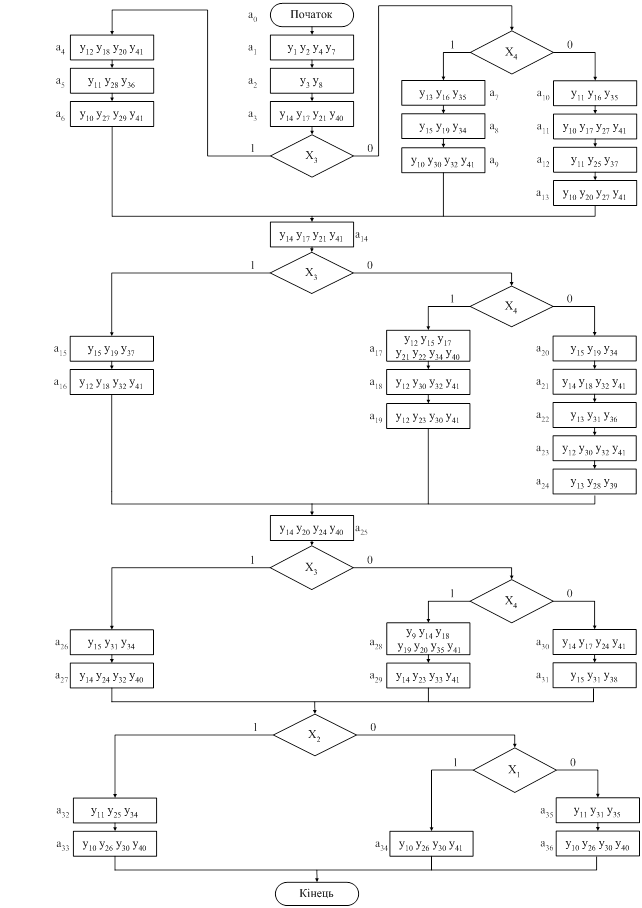 Рис. 2.2 – Граф-схема автомата Мура
Рис. 2.2 – Граф-схема автомата Мура