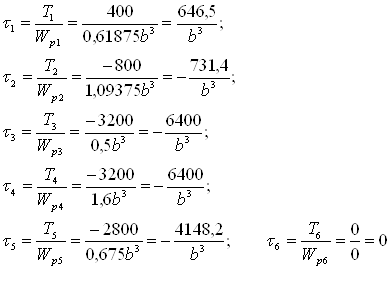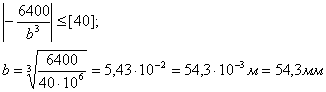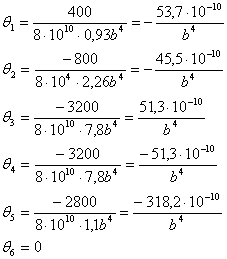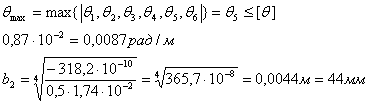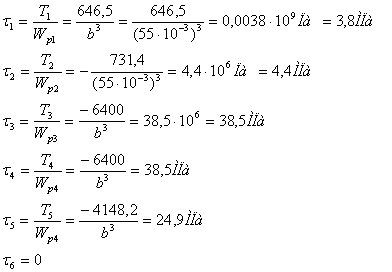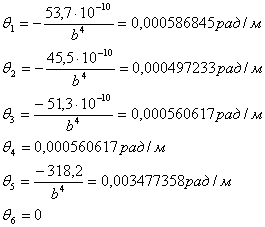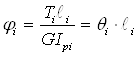Курсовая работа: СопроматКурсовая работа: СопроматЗадача № 1Тема: Расчет на прочность статически определимых систем при растяжении и сжатии Требуется: 1. Построить эпюру продольного усилия Ni 2.
По условию прочности подобрать размер поперечного сечение «а», если 3.
Для рассчитанного размера поперечного сечения построить эпюру нормальных
напряжений 4.
Построить эпюру осевых перемещений W и найти наибольшую величину относительных деформаций 5. Определить потенциальную энергию упругих деформаций U
Р1 = 50 кН; l1 = 3 м ; Øa 2a Р2 =65 кН; l2 = 2 м ; Ø2a a 2a Р3 =40 кН; l3 = 3 м ; a Р4 =10 кН; l4 = 1м ; D C B A Формы сечения: Ra P4 P3 P2 P1 А1 № 11 А3 № 4 А2 № 9 А4 № 7 IV III II I l 1 l2 l3 l4 Ni = ? ;
15 + Эп.N (kH) - 16 50 3,69 2 + Эп.σ(МПа) -
13 1,99 2,986 3,534 6,9 0 Эп.∆l(мм) + Решение: Определяется сила реакции опор RА из уравнения статики:
Делим на 4 участка, обозначая их римскими цифрами (I, II, III, IV), а также характерные сечения через заглавные буквы (А, В, С, D, Е). Определяется продольная сила на каждом участке методом сечения:
Строится эпюра продольных сил Ni Определяется площадь поперечных сечений на каждом участке А1=а*а=а2 А2=2а*а=2а2 А3=2а*2а=4а2
Определяется нормальное напряжение на каждом участке через 1/а2
Определяется
максимальное значение нормального напряжения, не превышающее допускаемого
напряжения, равное 160 МПа: Максимальное
значение напряжения на третьем участке Находится значение «а»:
Принимается а = 19,4мм Определяются действительные значения площадей поперечных сечений:
Определяются истинные значения нормального напряжения на каждом участке:
10.
Строится эпюра нормального напряжения 11. Определяется относительная продольная деформация на каждом участке:
12.
Определяется относительная продольная деформация
13.
Определяется относительное удлинение
Определяется
максимальное значение относительного удлинения: 14. Определяется удельная потенциальная энергия
15. Определяется полная удельная потенциальная энергия
16. Определяется относительная погрешность нормального напряжения:
Задача №2Тема: Расчет на прочность статически неопределимых систем при сжатии и растяжении Дано: Схема бруса Размеры и нагрузки Материал брусьев – сталь 3 Допускаемое
напряжение Модуль
продольной упругости Требуется: Определить допускаемую нагрузку для ступенчатого бруса
l = 30 см = 0,3 м = 300 мм А = 10 см2 = К = 0,15
[Р] = ? Эп. N (kH) Эп. σ (kH) Эп. l (мм) Ra + - + - + -
A A 1.5l 3A I 255 53 0,02
B 2A II 133 В l 0,047 C C 425 С 1.5l 4P 4A III 66,4 0,066 D D l A IV 255 159 E 0,035 E ∆ Re Решение: Составляется уравнение статики
Составляется уравнение совместности деформации УСД:
Определяются продольные силы на каждом участке:
Находим относительное удлинение на каждом участке
Определяется
Подставляем
значения
Подставляем
значение силы Определяем
значения продольных сил, подставляя значения
Определяется
значение нормального напряжения на каждом участке
Находим максимальное значение нормально напряжения
Принимаем Р = 170 кН Определяются действительные значения продольных сил:
10.
Определяются истинные значения нормального напряжения на каждом участке
Находим
относительное удлинение
Находим
относительное удлинение по сечениям
Определяем
относительное удлинение
По
заданной формуле вычисляем значение зазора
Проверка
Задача № 3 Тема: Расчет на прочность статически неопределимых систем при растяжении и сжатии. Требуется: Найти усиление и напряжение в стержнях, выразив через силу Р1 Определить допускаемую нагрузку [Р], если [σ] = 160 МПа Найти предельную нагрузку Рпр, если [σ1] = 240 МПа и h1 = 1,5 Сравнить величины допускаемых нагрузок Рпр и Р, для чего найти их отношения.
Дано: А=14см2 = 14·10 - 4м а=2,3м
с=1,7см [σ] =160 МПа hТ = 1,5
Найти: Р=?, РТ =?, [РТ] =? Решение. 1. Составляется уравнение статики для стержневой системы 1. Σ Мi = 0; Ν1·a-P(a+c) +N2cos 45·b =0 2. Σ Zi =0; Z0 +Ν2· cos45 = 0 3. Σ Yi =0; Y0 + Ν1– P - N2·cos 45 = 0 В три уравнения равновесия входят четыре неизвестные силы, и, следовательно, задача является статически неопределимой. Для составления уравнения рассмотрим деформацию конструкции. 2.
Рассмотрим подобие двух треугольников Рассмотрим
OB=b OA=a
B1 ∆l1 B2 O A B A1 ∆l2
3.
Подставляем
4. Находим значения нормальных напряжений σ1, σ2 σ1
= σ1
=
Принимаем 5. Находим действительные значения Ni
6. Находим действительные значения σi σ1
= σ2
= 7. Определяем предельную нагрузку Pпр, исходя из условия равновесия Σ Мi = 0; Ν1·а– Р·(a+c) + N2cos 45·b =0, где N1 = σт · А, и N2 = σт · 2А; σт=240МПа
8. Находим предельно допускаемую нагрузку
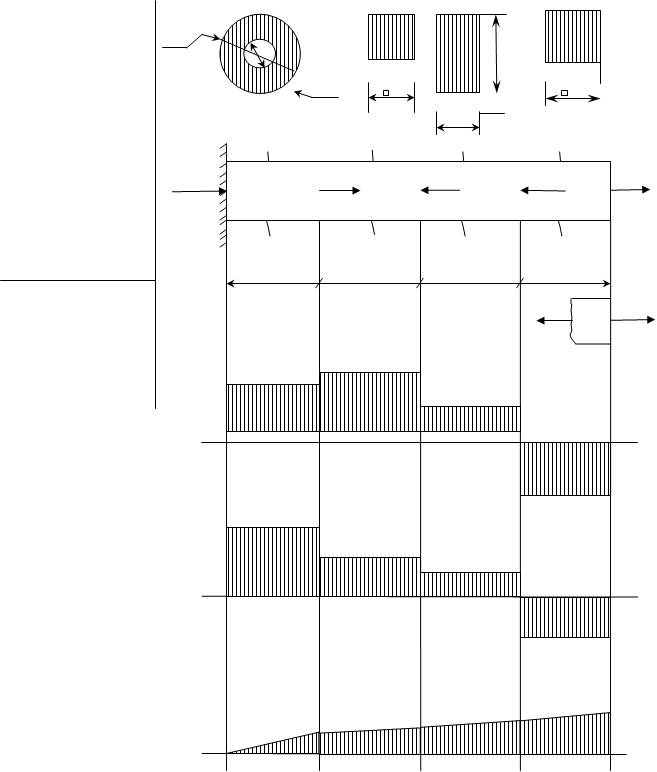
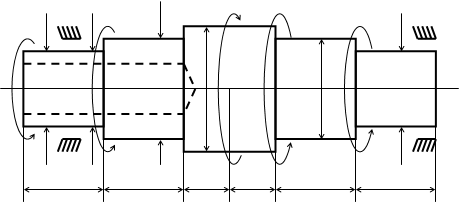
Задача № 4 Тема: Расчет статически определимых брусьев на прочность и жесткость при кручении. Дано: Схема бруса. Размеры нагрузки. Требуется: Рассчитать брус на прочность и жесткость Построить эпюры крутящих моментов, касательных напряжений и углов поворота.
m1 = 400 Н∙м m2 = 1200 Н∙м m3 = 2400 Н∙м m4 = 400 Н∙м m5 = m5 Н∙м [τ] = 40 МПа [θ]
= 0,5 d = 0,5 d1 = 1.5b d2 = 2b d3 = 2.5b
Найти: Т, τ, θ - ? Решение. Составим уравнение статики: Σ Мi = 0 m1 – m2 – m3 + m4 + m5 = 0 m5 = - m1 + m2 + m3 – m4 = - 400 + 1200 + 2400 – 400 = 2800 H·м T1 = + m1 = 400 H·м T2 = m1 – m2 = 400 – 1200 = - 800 H·м T3 = m1 – m2 – m3 = - 800 – 2400 = - 3200 H·м T4 = m1 – m2 – m3 = - 800 – 2400 = - 3200 H·м T5 = m1 – m2 – m3 + m4 = – 2800 H·м T6 = m1 – m2 – m3 + m4 + m5 = 0 H·м Определяем полярный момент сопротивления на каждом участке Wpi:
Определяется
касательное напряжение на каждом участке по формуле
Определяем максимальное значение касательного напряжения из пяти значений: τmax = max {τ1, τ2, τ3, τ4, τ5} ≤ [τ] ; τ3 ≤ [τ]
Определяется
полярный момент инерции по данной формуле
5. Определяем относительный угол закручивания по формуле
Определяем максимальное значение:
Примем максимальное значение из полученных значений b: b≥ = b1 = 54,3 мм = 54,3·10 - 3 м = 55мм 6. Определяем действительные значения касательного напряжения τi:
Определяем действительные значения относительного угла закручивания θi:
Определяем по формуле значение перемещения
Находим числовые значения перемещения Δφi по сечениям: φА = 0 φВ = φА + φ1 = 0 + 0,000176053 = 0,000176053 рад; φС = φВ + φ2 = 0,000176053 + 0,000149169 = 0,000325222 рад; φD = φС + φ3 = 0,000325222 + 0,000168185 = 0,000493407 рад; φЕ = φD + φ4 = 0,000493407 + 0,000168185 = 0,000661592 рад; φF = φЕ + φ5 = 0,000661592 + 0,003477358 = 0,00413895 рад; φG = φF + φ6 = 0,00413895 + 0= 0,00413895 рад. |
|||||||||||||||
 Дано: 7
Дано: 7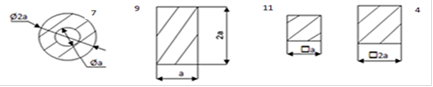
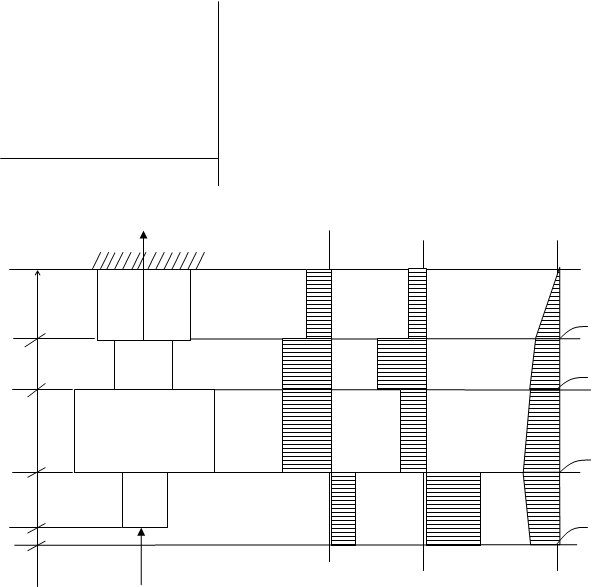 Дано:
Дано: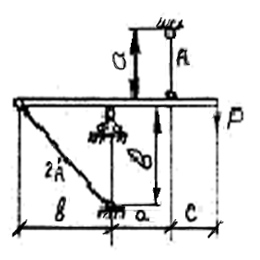

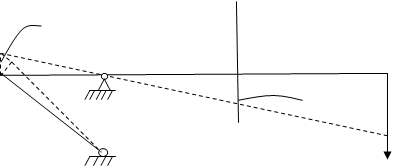
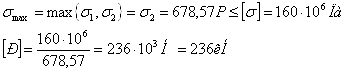
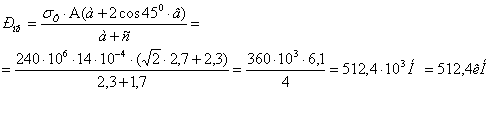
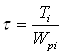 , выражая каждое значение через
1/b3
, выражая каждое значение через
1/b3