Курсовая работа: Тяговый и динамический расчет автомобиля ГАЗ-4301Курсовая работа: Тяговый и динамический расчет автомобиля ГАЗ-4301Содержание Введение. 1 Краткая техническая характеристика. 2 Оценка тягово-скоростных характеристик. 2.1 Уравнение движения автомобиля. 2.2 Внешняя скоростная характеристика двигателя. 2.3 Тяговая характеристика автомобиля. 2.3.1 Радиус качения. 2.3.2 Расчет кинематической скорости автомобиля по передачам. 2.3.3 Коэффициент полезного действия трансмиссии. 2.3.4 Расчет касательной силы тяги на ведущих колесах автомобиля. 2.3.5 Сила сопротивления дороги. 2.3.6 Сила сопротивления воздуха. 2.3.7 Практическое использование тяговой характеристики автомобиля. 2.4 Мощностная характеристика автомобиля. 2.5 Динамическая характеристика автомобиля. 2.6 Разгон автомобиля. 2.6.1 Коэффициент вращающихся масс. 2.6.2 Ускорение автомобиля при разгоне. 2.6.3 Определение времени разгона автомобиля 2.6.4 Определение пути разгона автомобиля 3. Топливная экономичность автомобиля 3.1 Построение топливной характеристики автомобиля. Литература. Введение При разработке и доводке конструкций автомобилей ЗиЛ наиболее серьезное внимание, помимо технологичности, уделялось их долговечности, надежности, безопасности, облегчению управления, повышению плавности хода в снижению затрат труда на техническое обслуживание в ремонты в процессе эксплуатации. В процессе работы над созданием автомобилей в основу были положены опыт отечественного автомобилестроения, тщательный анализ и исследование ряда современных моделей зарубежных грузовых автомобилей подобного класса, широкая постановка научно-исследовательских и опытно-конструкторских работ по рабочим процессам, системам и элементам конструкций. В широких масштабах осуществлялся поиск оптимальных мощностных, размерных и конструктивных вариантов. С точки зрения потребителя, модели автобусов ГАЗ обладают рядом преимуществ. Они динамичны, улучшена их устойчивость, легки в управлении в любых дорожных и климатических условиях. Рассматриваемый в данной работе грузовой автомобиль ГАЗ 4501 — средней грузоподъемности. 1. Краткая техническая характеристика Таблица 1.1 – Техническая характеристика автомобиля ГАЗ 4301.
2. Оценка тягово-скоростных характеристик 2.1 Уравнение движения автомобиля Оценку тягово-скоростных свойств автомобиля производят, решая уравнение его движения. Уравнение движения автомобиля связывает силу, движущую автомобиль, с силами сопротивления и позволяет определить характер прямолинейного движения автомобиля, т. е. в каждый момент времени найти ускорение, скорость, время движения и пройденный автомобилем путь. Окружная
сила на ведущих колесах
Здесь знак
"-" при силе Решение уравнения движения автомобиля в общем виде аналитическими методами практически невозможно, так как неизвестны точные функциональные зависимости, связывающие силы, действующие на автомобиль, с его скоростью. Поэтому уравнение движения автомобиля (2.1) решают численными методами на ЭВМ или приближенно, используя графоаналитические методы. Наибольшее распространение получили метод силового (тягового) баланса, метод мощностного баланса и метод динамической характеристики. 2.2 Внешняя скоростная характеристика двигателя Скоростная характеристика может быть построена расчетным путем по эмпирическим зависимостям, либо по данным, полученным в результате стендовых испытаний двигателя. В данном курсовом проекте для получения скоростной характеристики мы используем эмпирические зависимости. Построение
кривых скоростной характеристики ведется в интервале частот вращения
коленчатого вала от Определим
интервал частот вращения коленчатого вала для двигателя. Минимальные устойчивые
обороты автомобиля
Расчетные
точки кривой эффективной мощности определяются по формуле Лейдермана через
каждые 440 где Коэффициенты
где
При этом
соблюдается равенство Производим вычисление значений эффективной мощности двигателя для выбранных частот вращения коленчатого вала. Результаты вычислений сводим в таблицу расчетов внешней скоростной характеристики (см. табл. 3.2). Расчетные
точки кривой эффективного крутящего момента определяются через каждые 440
где Производим вычисление значений эффективного крутящего момента двигателя для выбранных частот вращения коленчатого вала. Результаты вычислений сводим в таблицу расчетов внешней скоростной характеристики (см. табл. 3.2). Условия
работы двигателя, установленного на автомобиле, отличаются от стендовых:
двигатель работает с другими впускными и выпускными системами, на нем
устанавливаются дополнительные механизмы, на привод которых затрачивается
определенная мощность, двигатель работает при другом температурном режиме.
Поэтому мощность двигателя, установленного на автомобиле При
использовании для тягово-скоростных расчетов стендовой внешней скоростной
характеристики, значения мощности В
приближенных расчетах можно принимать Зависимости
мощностей Результаты расчетов сводятся в табл. 2.1. Таблица 2.1 – Показатели внешней скоростной характеристики.
Рисунок 2.1 – График внешней скоростной характеристики. 2.3 Тяговая характеристика автомобиля 2.3.1 Радиус качения Для определения движущей силы автомобиля необходимо знать величину радиуса качения ведущего колеса. Так как на колесах автомобиля установлены эластичные пневматические шины, то величина радиуса качения колес во время движения изменяется. Радиус
качения характеризует путь, пройденный колесом за один оборот. Он соответствует
радиусу такого фиктивного жесткого колеса, которое при отсутствии
пробуксовывания и проскальзывания имеет одинаковую с действительным колесом
угловую Радиус качения колеса зависит от нормальной нагрузки, внутреннего давления воздуха в шине, окружной силы, коэффициента сцепления колеса с дорогой и поступательной скорости движения колеса при его качении. Расчетный
радиус качения
где
Приближенно
статический радиус шины
где
Расчетный
радиус качения
2.3.2 Расчет кинематической скорости автомобиля по передачам Кинематическая скорость автомобиля является функцией от угловой скорости коленчатого вала двигателя, и определяется выражением:
где Радиус колеса
Передаточное
число главной передачи Передаточные числа каждой передачи коробки берем также из табл. 1.1 Теперь производим расчет значений кинематической скорости автомобиля для каждой угловой скорости коленчатого вала двигателя на каждой из передач. Расчет производим по формуле (2.9). Результаты сводим в таблицу (см. табл. 2.2). 2.3.3 Коэффициент полезного действия трансмиссии При определении коэффициента полезного действия (КПД) трансмиссии учитывают гидравлические потери, вызванные взбалтыванием и разбрызгиванием масла в картерах коробки передач и ведущего моста, и механические потери, связанные с трением между зубьями шестерен, в подшипниковых узлах и в карданных шарнирах. В общем
случае КПД трансмиссии
где к, 1, m и n -
соответственно число пар цилиндрических шестерен внешнего зацепления ( В расчетах
принимают: При работе трансмиссии
с полной нагрузкой, т. е. при работе двигателя по внешней скоростной
характеристике, КПД трансмиссии имеет следующие значения: грузовые автомобили и автобусы - 0,83 ... 0,86; грузовые автомобили повышенной проходимости - 0,80 ... 0,85. Большие значения КПД трансмиссии относятся к прямой передаче в коробке передач автомобиля. Принимаем 2.3.4 Расчет касательной силы тяги на ведущих колесах автомобиля Касательная сила тяги на ведущих колесах автомобиля определяется выражением, Н:
где Производим расчет значений касательной силы тяги на ведущих колесах автомобиля по формуле (2.13) для каждой из передач. Результаты сводим в таблицу 2.2. На графике строим кривые в зависимости от скорости (рис 2.2) Таблица 2.2 Кинематическая скорость и касательная сила тяги.
2.3.5 Сила сопротивления дороги Сила
сопротивления качению колес автомобиля
где Коэффициент
сопротивления качению Коэффициент Коэффициент
где Значения В нижней
части графика тяговой характеристики автомобиля (рис. 2.2) наносим кривую 2.3.6 Сила сопротивления воздуха Сила
сопротивления воздуха
где Коэффициент
сопротивления воздуха принимаем Лобовую
площадь автомобиля принимаем Значения
Кривую силы
сопротивления воздуха Таблица 2.3 – Сила сопротивления дороги и сила сопротивления воздуха.
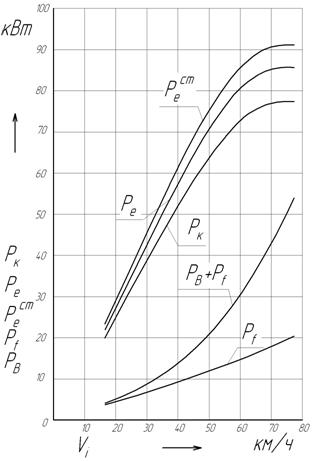
Рисунок 2.2 – Тяговая характеристика автомобиля. 2.4 Мощностная характеристика автомобиля Рассчитываем мощность, подводимую от двигателя к ведущим колесам автомобиля:
Заносим
данные в соответствующие строки табл. 2.4 и строим зависимость Рассчитываем мощности затрачиваемые на преодоление силы воздуха и силы сопротивления дорожного покрытия:
Заносим
данные в соответствующие строки табл. 2.4 и строим зависимости Отношение мощности, необходимой для равномерного движения автомобиля (
Значения степени использования мощности двигателя И также заносим в табл. 2.4. Таблица 2.4 – Показатели мощностной характеристики.
Рисунок 2.3 – График мощностной характеристики. 2.5 Динамическая характеристика автомобиля Методы тягового (силового) и мощностного балансов затруднительно применять при сравнении тягово-динамических свойств автомобилей, имеющих различные снаряженные массы и грузоподъемность, так как при движении их в одинаковых условиях силы и мощности, необходимые для преодоления суммарного дорожного сопротивления, различны. От этого недостатка свободен метод решения уравнения движения с помощью динамической характеристики. С этой целью
воспользуемся безразмерной величиной D - динамическим фактором, равным отношению свободной силы тяги (
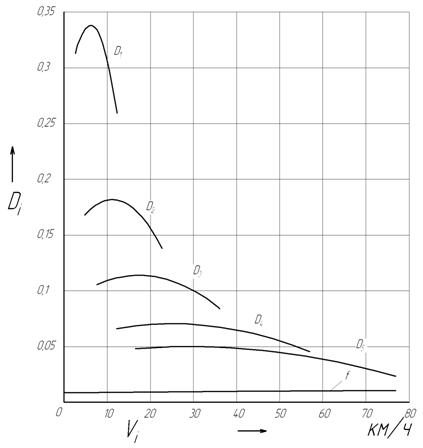
Значения динамического фактора заносим в табл. 2.5. Графическое изображение зависимости динамического фактора от скорости движения автомобиля на различных передачах в коробке передач и полной нагрузке на автомобиль называют динамической характеристикой автомобиля, т. е. D = f(V) (рис.2.4).
Рисунок 2.4 – График динамической характеристики. 2.6 Разгон автомобиля Время равномерного движения автомобиля обычно невелико по сравнению с общим временем его работы. При эксплуатации в городах автомобили движутся равномерно всего 15 -20 % времени, 40 - 45 % - ускоренно и 30 - 40 % - замедленно. Показателем динамических свойств автомобиля при разгоне служит интенсивность разгона или приемистость автомобиля. Приемистость (интенсивность разгона) автомобиля характеризует его способность быстро трогаться с места и увеличивать скорость движения. Это свойство автомобиля имеет особенно большое значение в условиях городского движения при частых остановках и троганиях с места, а также характеризует быстроту осуществления обгонов в условиях загородного движения. Интенсивность разгона автомобиля измеряется величиной его ускорения. 2.6.1 Коэффициент вращающихся масс Коэффициент учета вращающихся масс.
где Рассчитываем коэффициенты учета вращающихся масс по формуле (2.20) для каждой передачи. Результаты сводим в таблицу 2.5. 2.6.2 Ускорение автомобиля при разгоне Ускорение автомобиля определяют экспериментально или рассчитывают применительно к горизонтальной дороге с твердым покрытием хорошего качества при условии максимального использования мощности двигателя и отсутствии буксования колес. Трогание автомобиля с места кратковременно и определяется преимущественно индивидуальными особенностями водителя. Поэтому считают, что разгон начинается с минимальной скорости Vmin на передаче, с которой происходит трогание автомобиля с места. Величину ускорения в м/с находят из уравнения (2.21):
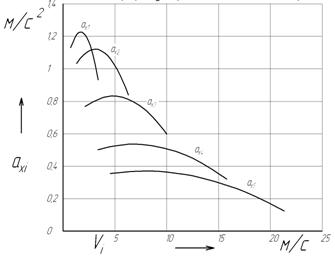
где Значения ускорения для каждой передачи заносим в табл. 2.5. Строим график ускорений автомобиля на передачах (рис. 2.5) в зависимости от скорости его движения.
Рисунок 2.5 – График ускорения автомобиля. Таблица 2.5 – Показатели тяговой характеристики автомобиля.
2.6.3 Определение времени разгона автомобиля Трогание с места начинают на передаче, обеспечивающей максимальное ускорение. Для определения наиболее интенсивного разгона в расчет вводят ускорения, соответствующие максимально допустимой скорости движения автомобиля на данной передаче. Время
разгона автомобиля на
Интегрирование последнего выражения производят численным методом. С этой целью кривые ускорения на каждой из передач разбивают на 5-6 одинаковых интервалов. Предполагается, что в интервале скорости:
где Ввиду
малости последнего, автомобиль движется равноускоренно с ускорением
Для повышения точности расчета интервал скоростей выбирают равным 3 ... 5 км/ч на низшей передаче, т. е. на передаче, с которой происходит трогание автомобиля с места, 5 ... 10 км/ч – на промежуточных и 10 ... 15 км/ч – на высшей передаче. Время
движения автомобиля
Общее время
разгона автомобиля на k-ой передаче
от скорости
где По
накопленным значениям Падение скорости:
где Исходные данные и результаты расчета сводим в таблицу 2.6. 2.6.4 Определение пути разгона автомобиля Путь разгона автомобиля
Этот
интеграл также вычисляется численными методами. При равноускоренном движении в
интервале скоростей
и проходит путь
Путь разгона
автомобиля до заданной скорости определяется суммированием элементарных путей Общий путь
разгона автомобиля на k-ой передаче
от скорости
где Путь
где скорость Исходные данные и результаты расчета сводим в таблицу 2.6. Строим график рис.2.6. Таблица 2.6 – Результаты расчетов времени и пути разгона.
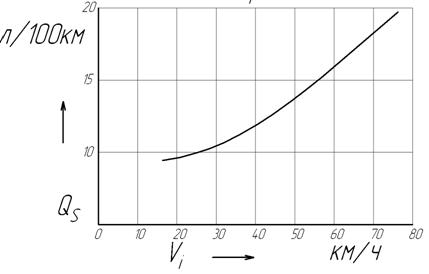
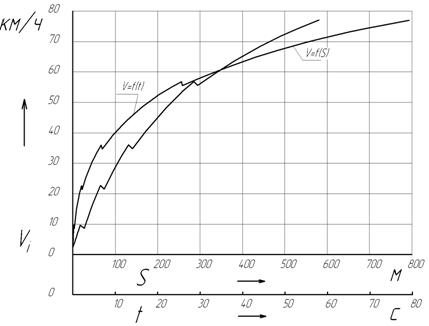
Рисунок 2.6 – График времени и пути разгона. 3. Топливная экономичность автомобиля 3.1 Построение топливной характеристики автомобиля Топливной экономичностью называют совокупность свойств, определяющих расход топлива при выполнении автомобилем транспортной работы в разных условиях движения. Топливной характеристикой установившегося движения называют зависимость путевого расхода топлива от установившейся скорости при установившемся движении на ровной горизонтальной дороге на высшей передаче. При построении графика топливной характеристики установившегося движения для заданной скорости автомобиля на высшей передаче определяется: - обороты двигателя, соответствующие заданной в км/ч скорости:
- значение эффективной мощности на валу двигателя, соответствующее полученным оборотам двигателя:
- значение мощности, передающейся в трансмиссию автомобиля:
- значение мощности, подводимой к ведущим колесам автомобиля на высшей передаче:
- значения мощностей, затрачиваемых на преодоление сил дорожного сопротивления и сопротивление воздуха (здесь скорость в м/с):
- значения степени использования мощности И и частоты вращения Е:
- определяем коэффициенты, зависящие от степени использования двигателя и частоты вращения коленчатого вала двигателя:
- путевой расход топлива (в л/100 км) определяется по формуле:
где Результаты сводим в таблицу 3.1. Строим график 3.1. Таблица 3.1 – Показатели топливной характеристики автомобиля.
Рисунок 3.1 – График топливной характеристики. 4. Выбор параметров зубчатых колес и кинематический расчет коробки передач Основные размеры и масса коробки передач определяются главным образом
размерами зубчатых колес. Предварительно параметры зубчатых колес определяются
на основе метода аналогии и использования статистических данных, отражающих
длительную практику автостроения. Затем они уточняются по результатам
проверочных расчетов и испытаний. Главным размерным параметром является
межосевое расстояние На основании данных о выполненных конструкциях соосных трехвальных коробок передач с двумя степенями свободы и неразветвленным потоком межосевое расстояние (мм) может быть представлено как функция крутящего момента на вторичном валу:
где Коэффициент
Практически для выполненных конструкций ряд значений Принимаем После выбора межосевого расстояния назначаются ширина зубчатых венцов, модуль и угол наклона зуба. Требуемая жесткость конструкции, удовлетворительная сбалансированность сроков службы зубчатых колес и подшипников и умеренная металлоемкость имеют место при практически установившихся пропорциях основных элементов коробки передач. Поэтому ширина зубчатых венцов, а также длина коробки по картеру и габаритные размеры валов и подшипников, выраженные в долях межосевого расстояния, сохраняют для выполненных конструкций с типовой компоновкой высокую степень постоянства. Рабочая ширина зубчатых венцов
Нормальный модуль ( Принимаем Большинство зубчатых колес в коробках передач выполняются косозубыми с
целью уменьшения шума при работе и повышения прочности. Прямозубые применяются
обычно для передачи заднего хода, а в грузовых автомобилях — также и для первой
передачи. Угол наклона косозубых колес Принимаем Предварительно рассчитываем сумму чисел зубьев.
Уточняем угол наклона зубьев
Трехвальные коробки передач с двумя степенями свободы на каждой передаче,
кроме прямой и заднего хода, передают мощность последовательно через две пары
зубчатых колес — пару привода промежуточного вала с передаточным числом ип
и выходную пару данной передачи с передаточным числом иi. В этом случае задача по подбору чисел зубьев включает
также рациональное распределение передаточного числа коробки передач икп
= ип Дальнейшая последовательность расчета: zвм 1 = иi1 = zвм 1 / zвщ 1 ; иi1 = 40 / 12 = 3,333 ип = и1 / иi1 ; ип = 6,289 / 3,333 = 1,886 иi2 = и2 / ип ; иi2 = 3,391 / 1,886 = 1,798 = щ/ип; щ2 = и21и„; иа = щ1иа; ... После того как для каждой пары сопряженных зубчатых колес рассчитаны передаточные числа {и — иа, и = = «хЬ и = Ыг2, « = «гз, —), искомые числа зубьев 2ВЩ и 2ВМ определяются на основе решения системы (3.15). Числа зубьев округляются до целых значений, затем производится уточнение передаточных чисел. С целью приближения к заданному ик. п можно изменять ранее выбранное значение 22, компенсировав это изменение соответствующим смещением или корректировкой угла наклона р. Литература 1. Гришкевнч А.И. Автомобиль: Теория. - Ми.: Высш. шк., 1986. - 208 с. 2. Токарев А.А. Топливная экономичность и тягово-скоростные качества автомобиля. -М.: Машиностроение. 1982. - 224 с. 3. Конструирование и расчет колесных машин высокой проходимости: Расчет агрегатов и систем / Под ред. Н.Ф. Бочарова. Л.Ф.Жеглова. - М: Машиностроение, 1994. - 404 с. 4. ГОСТ 4754 - 97. Межгосударственный стандарт. Шины пневматические для легковых автомобилен, прицепов к ним. легких грузовых автомобилей и автобусов особо малой вместимости. Технические условия. - Минск: Межгосударственный совет по стандартизации, метрологии и сертификации. 1999. 5. ГОСТ 5513 - 97. Межгосударственный стандарт. Шины пневматические для грузовых автомобилей, прицепов к ним. автобусов и троллейбусов. Технические условия. - Минск: Межгосударственный совет по стандартизации, метрологии и сертификации, 1999. 6. Литвинов АС, Фаробин Л.Е. Автомобиль: Теория эксплуатационных свойств. - М.: Машиностроение. 1989. - 240 с. 7. Мошностной баланс автомобиля В.А. Петрушов. ВВ. Московкин. А.Н. Евграфов. -М.: Машиностроение. 1984. - 160 с. 8. Евграфов А.Н.. Высоцкий М.С., Титович А.И. Аэродинамика магистральных автопоездов. - Ми.: Наука и техника, 1988. - 232 с. 9. Евграфов А.Н.. Есеновскнй-Дашков Ю.К. Аэродинамические свойства автомобилей и автопоездов. Методы исследований. - М.: МГАУ. 1998. - 79 с. 10. Европейский Союз. Технические стандарты на автотранспортные средства. Директива Совета 93.53 ЕС от 25 июля 1996 года. Максимальные разрешенные габаритные размеры и нагрузки (веса) автотранспортных средств. 11. Грузовые автомобили: Проектирование и основы конструирования М.С. Высоцкий. Л.Х. Гилелес. С.Г. Херсонский. - М.: Машиностроение. 1995. - 256 с. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
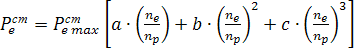 , (2.2)
, (2.2)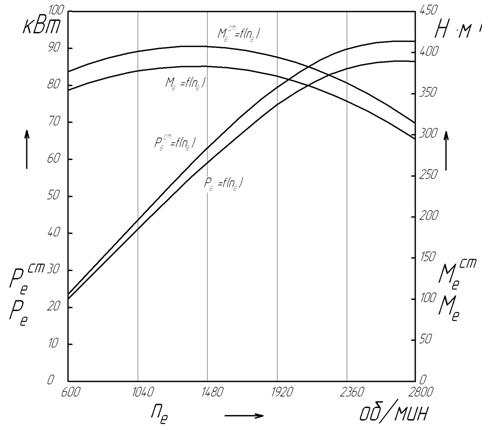
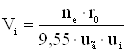 ;
;  ; (2.13)
; (2.13)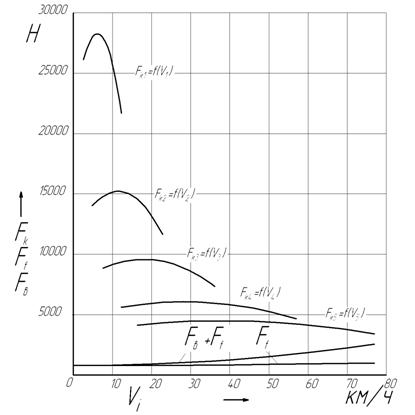
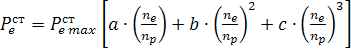 , (3.2)
, (3.2)